等幾何分析

等幾何分析（Isogeometric analysis）基於有限元分析方法的等參單元思想，將計算機輔助幾何設計（CAGD）中用於表達幾何模型的非均勻有理B樣條（NURBS）的基函式作為形函式，實現了計算機輔助設計（CAD）和計算機輔助工程（CAE）的無縫結合。

簡介

等幾何分析（Isogeometric analysis）方法基於有限元分析方法的等參單元思想，將計算機輔助幾何設計（CAGD）中用於表達幾何模型的非均勻有理B樣條（NURBS）的基函式作為形函式，實現了計算機輔助設計（CAD）和計算機輔助工程（CAE）的無縫結合。

等幾何分析著作

特點

由於NURBS基函式可以構造任意高階連續的近似函式，克服了有限元分析方法通常僅有C0連續性的弊端，使等幾何分析方法可以方便地求解薄板殼等高階問題。目前等幾何分析方法已成功用於固體、流體、電磁、振動和裂紋擴散等模型的分析，並展現出其相對有限元分析方法的很大優勢，如：無需進行幾何模型轉換，單元細分簡便且不損失幾何精度以及便於求解高階連續問題等。

在實現計算機輔助設計（CAD）和計算機輔助工程（CAE）結合的同時，等幾何分析方法也自然在結構最佳化中擁有了獨到的優勢。它可直接將幾何模型的NURBS控制點作為最佳化對象，並根據最佳化後的控制點坐標和權值簡便精確地得到最佳化後的形狀，而且最佳化後的邊界是光滑連續的NURBS曲線。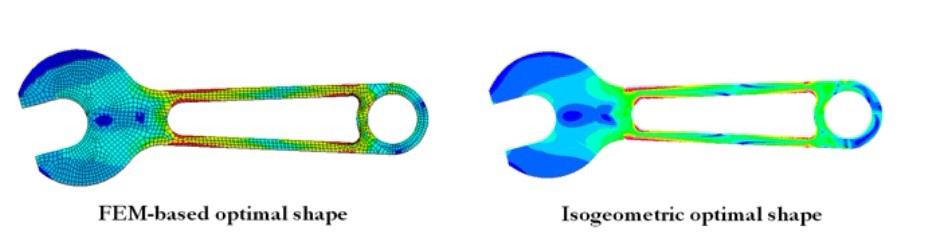

簡單示例

文獻給出了有關下面兩個算例的等幾何分析基礎理論和詳細實現流程。

結構分析

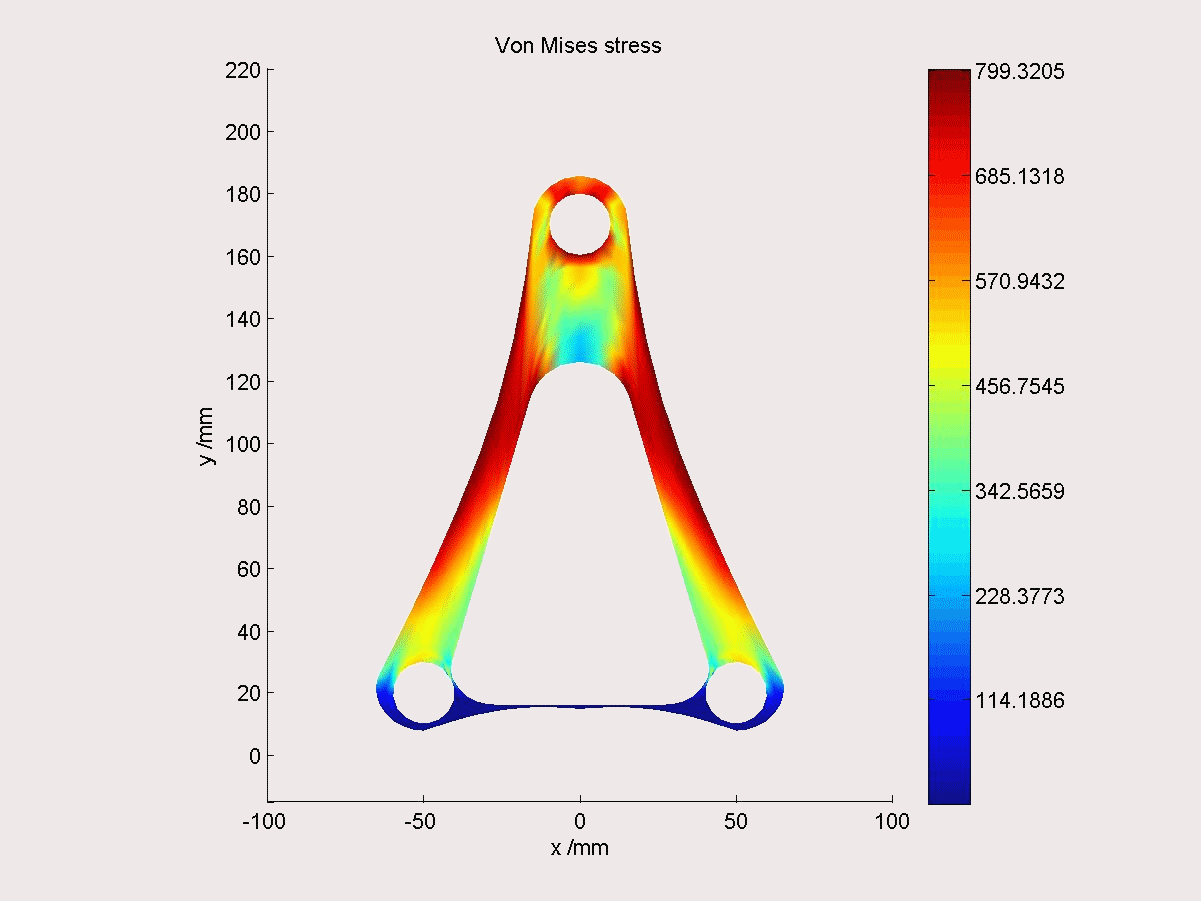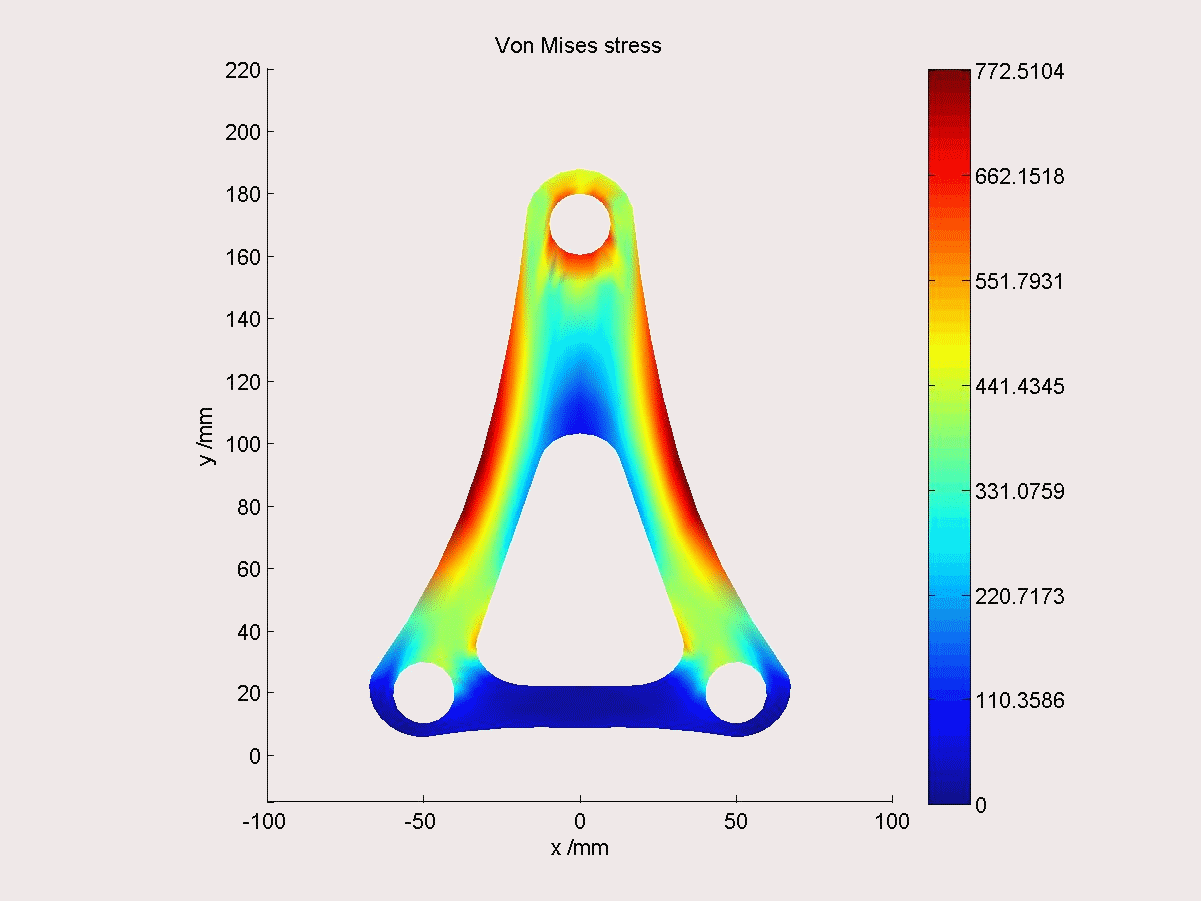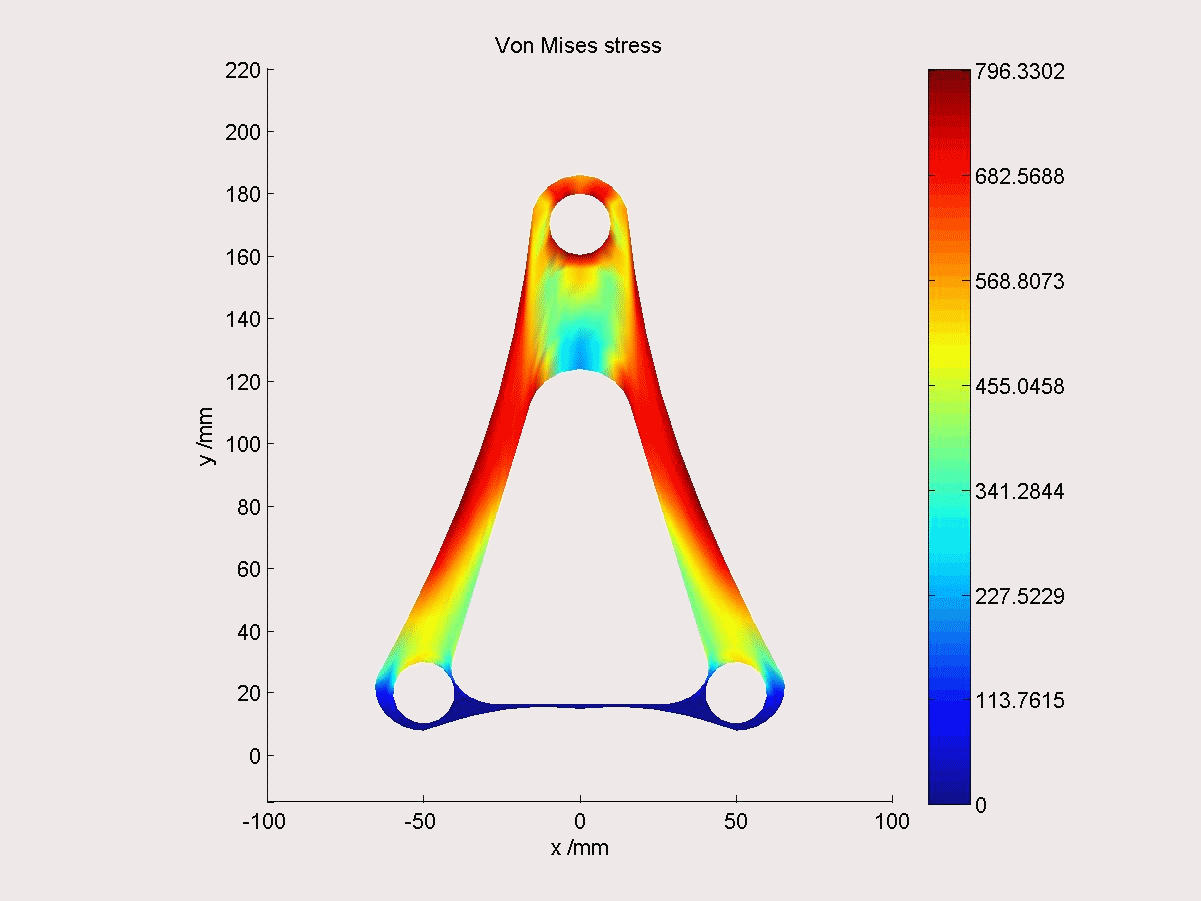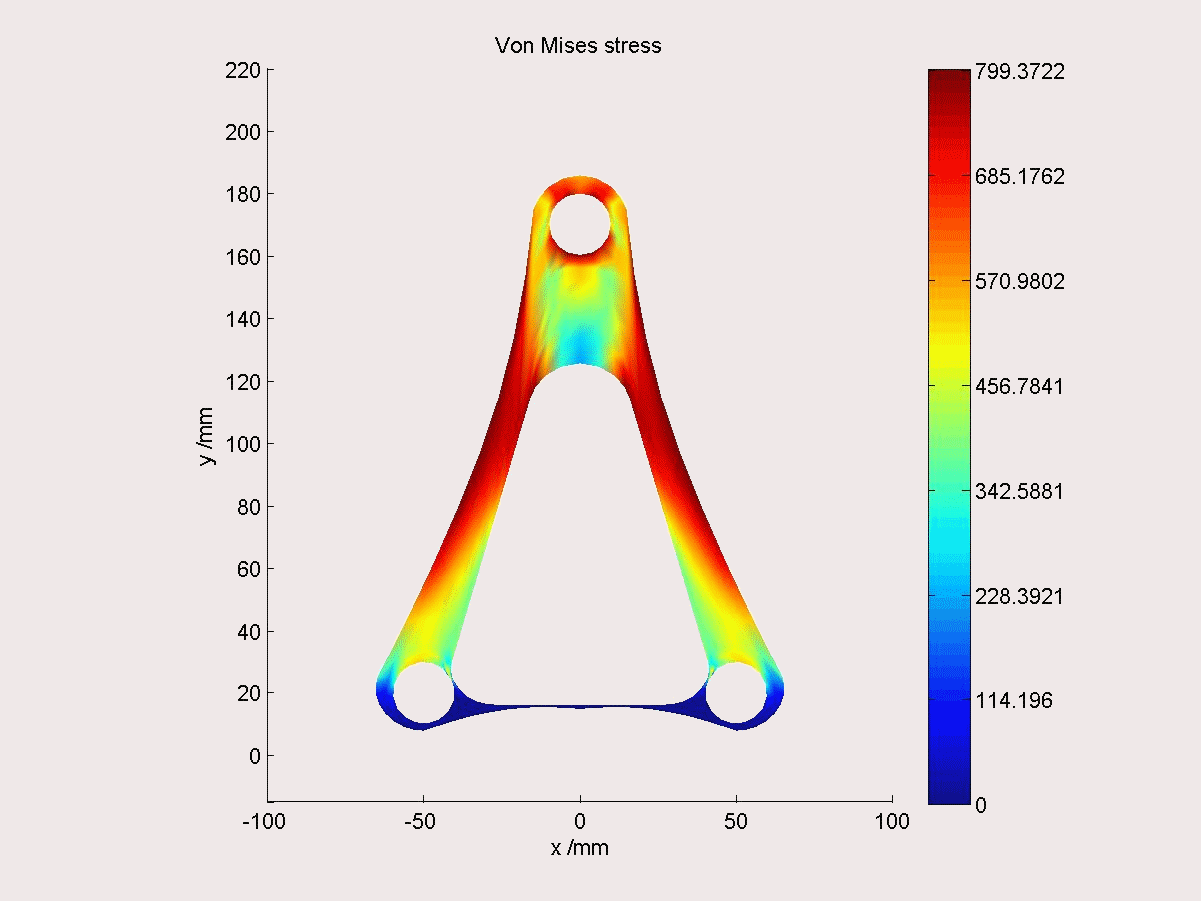
下圖為等幾何分析的分析示例，幾何模型在CAGD軟體Rhinoceros（犀牛）中建立，然後通過程式讀取模型信息並直接進行等幾何分析，中間無需進行模型轉換。圖中展示了結構幾何模型（左）、NURBS控制點格線（中上）、結構物理空間格線（中下）和Von mises應力雲圖（右）。

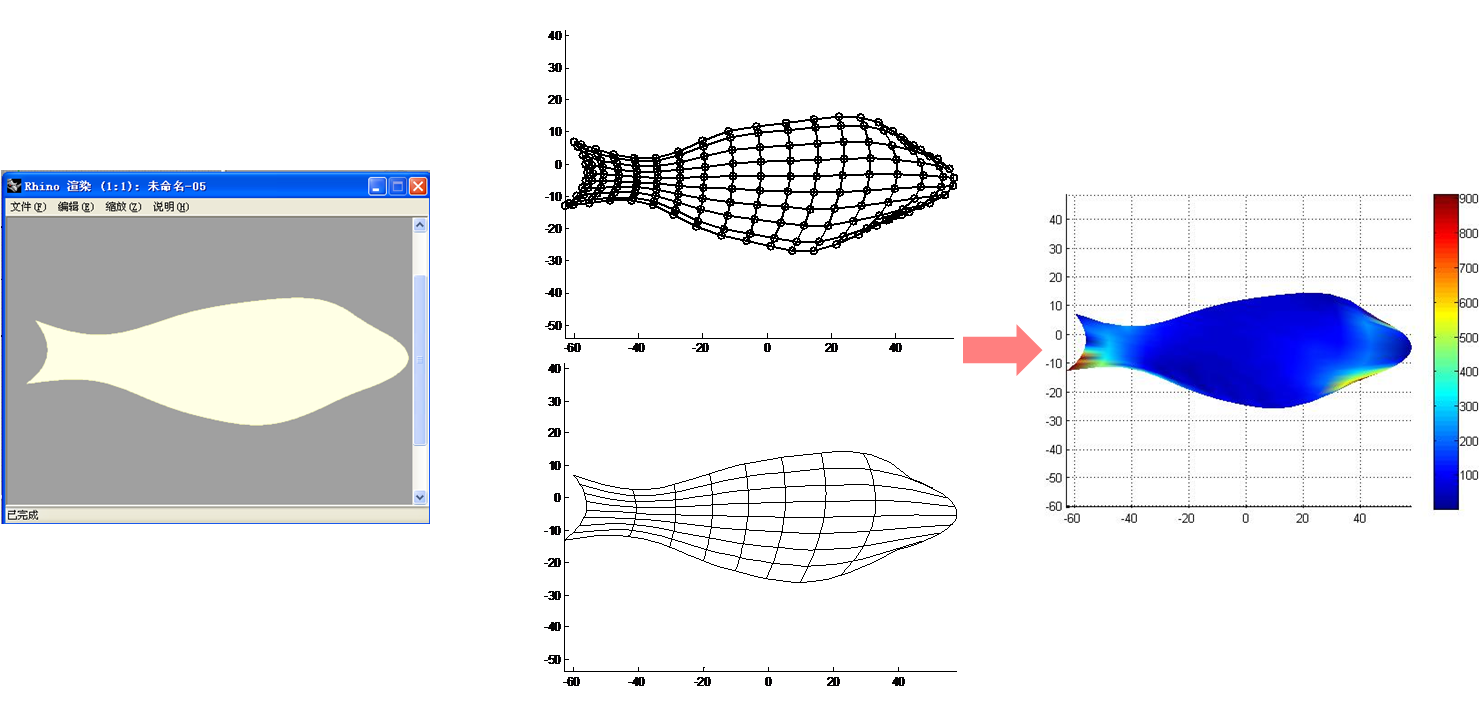
結構最佳化

下圖為等幾何分析的最佳化示例，幾何模型的NURBS控制點可直接作為結構最佳化變數。在應力約束下，以結構質量最小為目標，通過對控制點坐標的最佳化可快速得到支架的最優形狀。