基本介紹
- 中文名:等利潤曲線
- 外文名: Isoprofit curve
- 表示:能夠產生利潤水平所有投入品
- 員工福利:增長的相關經濟原理
基本定義,辨析,計算示例,
基本定義
等利潤曲線( Isoprofit curve) 等利潤曲線表示能夠產生某一利潤水平的所有投入品組合。 等利潤曲線圖
等利潤曲線圖
 等利潤曲線圖
等利潤曲線圖容易看出,等利潤曲線的斜率為-1。也就是說,一美元工資的削減將伴隨一美元福利的增加;無論廠商選擇支付曲線上哪一個工資和福利的組合,工人的總酬金以及企業的總利潤都將保持不變。
辨析
工人的無差異曲線
在圖中,I1、I2、I3代表工人的無差異曲線。每條無差異曲線都是所有能夠給工人帶來同等效用水平的工資和福利的組合的集合。不同的無差異曲線代表的效用水平也不同。從原點向右,每一條曲線代表的效用水平越來越高。
無差異曲線具有向下傾斜的特徵,是因為工資和福利都能給工人帶來效用,因此在一定程度上二者都能夠相互替代。這裡的問題在於:由於大多數福利是實物福利(In-kind Benefit),即體現為具體的產品或服務的福利,則對於同樣價值的工資和福利,一個工人(消費者)似乎更應該喜歡前者才對。因為消費者可以把一美元的現金工資以最喜歡從而也能給他帶來最大效用的方式花出去;而對於實物形式的福利,消費者就失去了這種選擇的自由。特別是,就具體的個人來說,實物的產品或服務可能並不會給他帶來多少實際利益。例如,對於一個沒有孩子的(或孩子都已長大成人的)工人來說,日托中心的服務可謂沒有絲毫價值。但是,確實存在這樣的理由,使得工人寧願犧牲一些工資,來換取一定數量的福利。分析如下:
首先,某些福利會使工人獲得更加有利的稅率。例如,對那些包含在私人養老計畫中的延遲的收入,工人們必須等到真正獲得這些收益時才會繳納稅收。既然當工人退休時不可能有工資收入,由養老金計畫提供的收入在納稅時就使用更低的邊際稅率(比如說15%),這比工人在工作期間獲得同樣數量的工資收入所適用的稅率(比如說28%或36%)要低得多。也就是說,養老金能夠通過收入延遲以少交稅率。類似的,由僱主支付的健康和人壽保險既不用繳納社會保險稅,也不用繳納個人所得稅。
其次,為防止自己過多地將收入滿足當前消費而忽略未來的利益,人們也願意用福利來代替一部分工資收入。人們可能意識到,他們的現金收入經常花在汽車、衣服、度假上。因此,接受包括福利在內的收入組合,實際上就相當於當前收入用於健康保險或是養老金方面,這樣在將來必要的時候,這些收入將會發揮更大的作用。 從圖1中還可以看到,無差異曲線不僅向右下方傾斜,而且還有向原點凸出的特徵。這說明,福利對工資的邊際替代率是遞減的。道理很簡單,若一個工人享有的福利較少,他將願意用較多的收入來換取額外一單位的福利。但隨著福利的增加,由福利帶來的邊際效用不斷降低,人們為增加一單位福利所願意放棄的工資收入就將變得越來越少。
僱主的等利潤曲線
給定產出水平,企業將盡力使每小時勞動的報酬最小化以實現最大利潤。在圖1中,WF及WF'為企業的等利潤曲線,該曲線上不同的工資和福利的組合都能給企業帶來一個既定水平的利潤量。為簡單起見,我們假設產品市場上的競爭導致了一個正常利潤;勞動市場上的競爭將迫使廠商支付一個由WF曲線表示的包括福利和工資的總酬金。也就是說,給定工資和福利的“價格”,WF上所有的點對應的工資和福利的組合都能夠使企業保有一個正常的利潤水平。容易看出,等利潤曲線的斜率為-1。也就是說,一美元工資的削減將伴隨一美元福利的增加;無論廠商選擇支付曲線上哪一個工資和福利的組合,工人的總酬金以及企業的總利潤都將保持不變。
工資—福利的最優組合
在圖1中,當WF與I2相切時,可以得出工資—福利的最優組合,它能使工人獲得最大效用。b點為等利潤曲線WF與無差異曲線I2的切點,對工人而言,該點的W0和F0的組合顯然是最好的,在這個點上,工人能夠實現效用的最大化。a和c 這樣的點雖然也在同一條等利潤曲線上,但它們帶來的效用I1顯然比b點的效用I2要小;當a、c兩點沿著等利潤曲線向b點不斷調整時,工人的效用就會持續增加。但在b點,此時不存在繼續調整以增加效用的餘地—也就是說,工資與福利的組合實現了最優。(由於偏好的差別,不同個人的無差異曲線通常也是不同的。我們假設這裡所考察的工人具有充分的代表性。
福利增加的理由
在圖1中WF′是一條比WF更平緩的正常利潤的等利潤曲線;與WF相比,WF'反映的福利的“價格”下降了。換句話說,在每一工資水平上,企業都能在不增加其總支出的前提下提供更多的福利,而且這種增加也不會削減企業的利潤。現在,廠商能夠用一美元的工資交換到價值一美元多的福利(儘管這些福利的成本只是一美元)。因此,為了吸引和保持高素質的員工,廠商將在WF′選取一點,作為提供給他們得更好的工資—福利組合(在競爭的勞動市場上,市場力量也將促使企業這么做)。 在圖1中,這條新的等利潤曲線與一條更高的無差異曲線I3切於一點d,該點表示新的工資和福利的最優組合。福利價格的降低促使工人“購買”更多的福利。與原來的組合(b點)相比,d點的組合中福利的比重明顯增加了。與此同時,工人的效用水平也由原來的I2增加到現在的I3。
企業增加員工福利的經濟原因
然而,是什麼導致了等利潤曲線的右移?什麼原因使福利的價格增加,並使得廠商能夠在薪金總額的利潤不變的前提下增加福利的數量。
原因分析如下:
對僱主有利的稅收。前面已經說明福利如何給工人帶來稅收上的利益。其實,福利同時也使僱主的稅收負擔變輕了。廠商可以通過改變總支出的構成來減輕自己的稅收負擔。例如,假設某個工人一年的收入為30000美元,按照2002年總工資稅的7.65%的稅率,僱主將不得不支付2295美元的稅收;如果僱主支付給工人20000美元的收入和10000美元的福利,那么雖然薪酬總額沒變,廠商的稅收負擔卻因此降至1530美元(20000×0.0765)。考慮到大公司通常擁有數量眾多的員工,新近構成的改變將能夠使他們節省一筆極為可觀的稅收支出。結果公司發現,現在它能夠為削減掉的每一美元的工資提供高於一美元的福利的補償。看到正常利潤的等利潤曲線由原來的WF向右移至WF′的位置。
計算示例
假定一家企業生產兩種產品,x和y;生產單位產品x的利潤貢獻為4萬元,生產單位產品y的利潤貢獻為6萬元。企業使用三種投入要素A,B和C。生產單位產品x要耗用A5個單位,B8個單位(生產產品x不需要耗用C)。生產單位產品y要耗用A10個單位,B6個單位和C10個單位。企業共擁有A50個 單位,B48個單位和C40個單位。這樣,可列出目標函式和約束條件如下。
目標函式:Z=4x+6y
約束條件:5x+10y≤50?
8x+6y≤48
10y≤40
x,y≥0
可以用圖解法和單純形法來解線性規劃問題。圖解法比較簡單,但套用面較窄;單純形法較為複雜,但套用面較廣。由於一般經濟數學課都要詳細涉及解線性規劃問題的方法,這裡只對圖解法做簡單的介紹,目的是為了更好地理解這種決策的原理和方法。
圖解法只適用於目標函式中只有兩個變數的情況,因為超過兩個變數就無法作圖。
圖解法的第一步是確定可行區域。
每一條約束條件都可以用來說明當某種投入要素得到充分利用時,產品x和產品y的最大可能的產量。例如,如果投入要素A得到充分利用,那么,投入要素A的約束條件就變成等式:
5x+10y=50
當 x=0時,y=5;
當 y=0時,x=10。
即如果所有投入要素A都用來生產產品y,可生產5個單位;都用來生產產品x,可生產10個單位。在連線這兩種產量組合的直線上的任何一點,都代表當投入要素A得到充分利用時,x產品和y產品最大可能產量的組合。約束方程5x+10y=50,把x、y的所有組合分成兩半。在方程的較小區域內的任何點,都能滿足5x+10y≤50的要求,在方程的較大區域內的任何點,都不能滿足上述約束條件的要求,因此,就投入要素A的約束條件5x+10y≤50來說,它的左側陰影部分才是可行區域。
同理,投入要素B的約束條件就變成等式:
8x+6y=48
當 x=0時,y=8;
當 y=0時,x=6。
投入要素C的約束條件就變成等式:
10y=40
這裡,y=4?
把這些約束條件的方程曲線畫出來,就能得到以各條約束條件方程直線為界限的區域,在這個區域內的所有的點,都能滿足約束條件提出的要求。這個區域就叫可行區域。?
圖解法的第二步是利用目標函式,在可行區域內找出產品x和產品y的最優產量組合,這種組合能保證企業利潤最大。
目標函式:
Z=4x+6y
或 y=z/6-2/3x
這是一條斜率為(-2/3)的直線,其位置則決定於Z的值。如果Z的值增加,這條直線就會平行外移。? 為了把目標函式畫在圖上,我們先隨意取一個Z值,譬如,Z=24。則?
目標函式:24=4x+6y?
或 y=4-2/3x?
當 x=0時,y=4;
當 y=0時,x=6。?
在直線4x+6y=24上,產品x和產品y的所有組合,都能使利潤達到24萬元,所以這條直線為等利潤曲線,然後從這等利潤曲線平行向外移動,一直到新的等利潤曲線與可行區域中在最外面的點相交時為止,這一點一般是可行區域的角點(除非目標函式的直線與約束條件的直線恰好平行)。在角點上的產品產量組合,就是能保證利潤最大的,即最優的產量組合。在本題中,這個產量組合為:x=3.6單位,y=3.2單位。把這兩個數字代入目標函式:?
Z=4x+6y=4×3.6+6×3.2?=33.6(萬元)?
產品x和產品y產量的任何其他可能的組合,都不會使利潤大於此數。
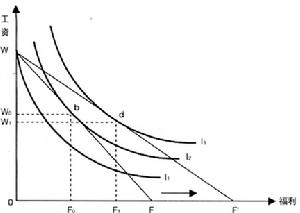 無差異,等利潤曲線圖
無差異,等利潤曲線圖