廣義的符號檢驗是對連續變數π分位點Qπ進行的檢驗;而狹義的符號檢驗則是僅針對中位數(或0.5分位點)M=Q0.5進行的檢驗。
基本介紹
定義
廣義
狹義
規定
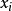
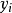


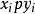





步驟
二項分布的P值
備選假設 | p值 | 使檢驗有意義的條件* |
H1:Qπ>q0 | PH0(K≤ s-) | Qπ>q0 |
H1:Qπ<q0 | 1-PH0(K≤ s- -1) | Qπ<q0 |
H1:Qπ≠q0 | 2min{PH0(K≤ s-),1-PH0(K≤ s--1)} |
說明
符號檢驗法

廣義的符號檢驗是對連續變數π分位點Qπ進行的檢驗;而狹義的符號檢驗則是僅針對中位數(或0.5分位點)M=Q0.5進行的檢驗。
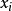
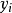


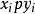





備選假設 | p值 | 使檢驗有意義的條件* |
H1:Qπ>q0 | PH0(K≤ s-) | Qπ>q0 |
H1:Qπ<q0 | 1-PH0(K≤ s- -1) | Qπ<q0 |
H1:Qπ≠q0 | 2min{PH0(K≤ s-),1-PH0(K≤ s--1)} |

名稱及概念sign test一種非參數檢驗方法。廣義的符號檢驗是對連續變數π分位點Qπ進行的檢驗;而狹義的符號檢驗則是僅針對中位數(或0.5分位點)M=Q0.5進行的...
威爾科克森符號秩檢驗亦稱威爾科克倫代符號的等級檢驗,是由威爾科克森(F·Wilcoxon)於1945年提出的。該方法是在成對觀測數據的符號檢驗基礎上發展起來的,比傳統的單獨...
亦稱威爾科克遜符號秩檢驗。一種非參數檢驗,適用於檢驗連續型變數配對觀測結果的齊一性,檢驗統計量基於各對觀測值之差的符號及其秩。 ...
在總體分布任意的情形下,檢驗配對的試驗數據所在總體的分布位置有無顯著差異,往往可以利用符號檢驗的方法實現。但是符號檢驗只考慮差數的正負號,而不考慮差數的絕對...
符號識別是自動識別領域裡最基本、最簡單的一種技術方法。用於識別的符號是人們特意為機器編制的一種專用圖象,它的最大特點就是便於機器自動識別。這種專用圖象,最...
成對比較檢驗是統計學分析中常用的比較分析方法,常用於對兩個相關樣本的比較分析,有符號檢驗和威爾科克森帶符號的等級檢驗兩種方法。成對比較檢驗也是食品感官檢驗中...
X2檢驗還可用於檢驗總體的次數分配是否屬於常態分配及進行成對資料的符號檢驗、兩組或兩組以上資料的中位數檢驗等。V百科往期回顧 詞條統計 瀏覽次數:次 編輯...
CAL,質量監督檢驗機構認證,是質量監督檢驗機構認證符號,國家授予的權威性標誌。...... CAL,質量監督檢驗機構認證,是質量監督檢驗機構認證符號,國家授予的權威性標誌。...
顯著性檢驗(significance test)就是事先對總體(隨機變數)的參數或總體分布形式做出一個假設,然後利用樣本信息來判斷這個假設(備擇假設)是否合理,即判斷總體的真實...
亦稱觀測結果隨機性檢驗、樣本隨機性檢驗。隨機性假設“n次觀測結果構成簡單隨機樣本”的一類統計檢驗。常用隨機性檢驗有:遊程檢驗,反演總數檢驗,遞差檢驗,遞差符號...
