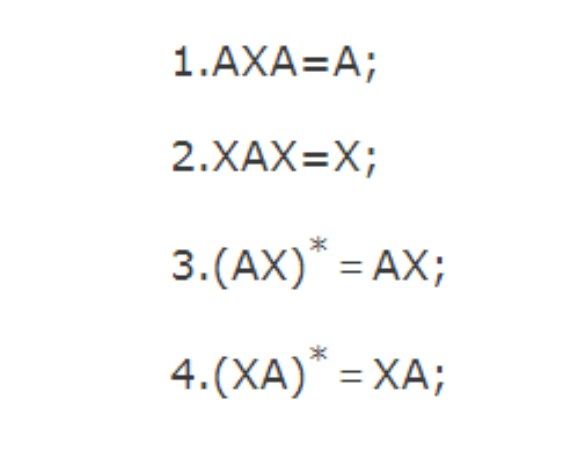穆爾-彭羅斯廣義逆矩陣(Moore-Penrose generalized inverse matrix)是逆矩陣概念的推廣，彭羅斯(R.Penrose)證明了對任一m×n階矩陣A，都存在惟一的n×m階矩陣X，它滿足：1.AXA=A；2.XAX=X；3.(AX)*=AX；4.(XA)*=XA；則稱X為A的穆爾-廣義逆矩陣，簡稱M-P逆，記為A。當A為n階非異陣時，其逆A也滿足條件1到4，故M-P逆確為通常逆矩陣的推廣。在矛盾線性方程組Ax=b的最小二乘解中，x=Ab是範數最小的的一個解，任意矩陣的廣義逆定義，最早是由穆爾(E.H.Moore)於1920年提出來的，根據實際問題的需要，一些學者還研究了其他各種類型的廣義逆矩陣。
基本介紹
- 中文名：穆爾-彭羅斯廣義逆矩陣
- 外文名：Moore-Penrose generalized inverse matrix
- 所屬學科：數學
- 所屬問題：高等代數(矩陣)
- 簡介：一種廣義逆矩陣
基本介紹,相關性質,相關說明,
基本介紹
1.AGA=A；
2.GAG=G；
3.(
)′=AG；
4.(
)′=GA，
則G稱為A的穆爾-彭羅斯廣義逆矩陣。顯然，A與G互為穆爾-彭羅斯廣義逆，任意的s×n復矩陣A有惟一的穆爾-彭羅斯廣義逆，記為A。
相關性質
矩陣A的廣義逆A有如下的性質：
1.A的秩r(A)=r(A)=r(A′)；
2.(A)=A；
3.(A′)=(A)′，因此，若A是對稱矩陣，則A+也是對稱矩陣；
4.(A′A)=A(A)′，因此，若A是半正定矩陣，則A也是半正定矩陣；
5.AA，AA都是冪等矩陣。
穆爾-彭羅斯廣義逆矩陣在最小二乘法中有用。
相關說明
設A為m×n的實矩陣，若n×m的矩陣H滿足下列條件：
AHA= A，HAH=H，(AH)=AH，(HA)T= HA (1)
則H稱為A的穆爾-彭羅斯廣義逆矩陣。該逆矩陣的唯一解通常表示為A。可證明，若對A進行奇異值分解，即：
A= USV，(2)
那么，根據正交矩陳的特性：
A= VSU， (3)
式中S是n×m的矩陣，
穆爾-彭羅斯廣義逆是很多廣義逆之一(Ben-Israel和Greville,1974)。也就是說，對當作逆的矩陣H有其它選擇，因而對問題Ax= b可得不同的近似解。例如，在阻尼最小二乘方法(或脊式回歸)中，矩陣H選為：
H= VFS+U (7a)
該式中F是n×n對角濾波矩陣，其分量為：
式中θ是大大小於最大奇異值σ1的調節參數。
該逆矩陣H的作用是產生估算值
,與穆爾-彭羅斯廣義逆的解所得的值相比，可能它的沿相應於最小奇異值的奇異矢量分量被阻尼了。可以證明該是下列問題的解：
對
求極小 (7c)
這樣就代表了在數據擬合和解的大小限制之間的折衷。這種思路也用於非線性最小二乘法，即大家熟知的利文伯格-馬今特法中(Levenberg-Marquardt method ) 。
與一般的逆矩陣不同，即使矩陣是奇異的，穆爾-彭羅斯的廣義逆矩陣總是存在的。在構成這種廣義逆矩陣時，必須小心地處理零奇異值。在式(6)中， 僅當σi>0時，定義σi=1/σi；而當σi= 0時，則定義σi=0。這就避免了一般求逆時由σi=1/σi帶來的問題。而且，奇異值可幫助理解矩陣的秩和矩陣的條件。
通常矩陣秩定義為最大互不相關的列數，這樣一個定義實際上很難套用於一般矩陣。然而若矩陣是三角形的，秩就是非零對角元素的數目。由於正交變換，比如在奇異值分解中的變換，並不影響秩，立即可以發現A的秩與其奇異值分解中S的秩相等，因此矩陣秩實用的定義是非零奇異值的數目。由於計算機精度有限，可能很難區別一個小奇異值和零奇異值，因而定義有效秩是大於某預定容限的奇異值數。容限反映了機器和數據的精度。
最後需指出，廣義逆的奇異值分解(SVD)方法為我們的問題提供了有效的分析手段。哥魯布和萊因思奇(Golub,Reinsch,1970)研究出奇異值分解的數值計算。在大多數計算中心，子程式庫中一般都有奇異值分解子程式。雖然奇異值分解分析比喬勒基(Cholesky)法解正規方程要化去較多計算機時間， 但這是很值得的。按乘法運算的實際計數，奇異值分解需2mn+4n，而正規方程方法則需mn/2 +n/6。 例如，若解300個未知數的1000個方程，奇異值分解分析所需要的計算機時間約比正規方程方法長6倍。
但這裡需指出正規方程方法的兩大缺點。第一，正規方程矩陣的條件數是原始矩陣條件數的平方。這樣，在組成正規方程和求解它時，需要把浮點精度t提高一倍才能避免計算中的舍人誤差。第二，正規方程方法不能計算信息密度矩陣。
