基本介紹
- 中文名:程式理論
- 外文名:theory of programs
- 學科:計算機科學
- 定義:研究程式的語義和設計
- 組成:程式語義理論、數據類型理論等
- 有關術語:程式
簡介
有關理論
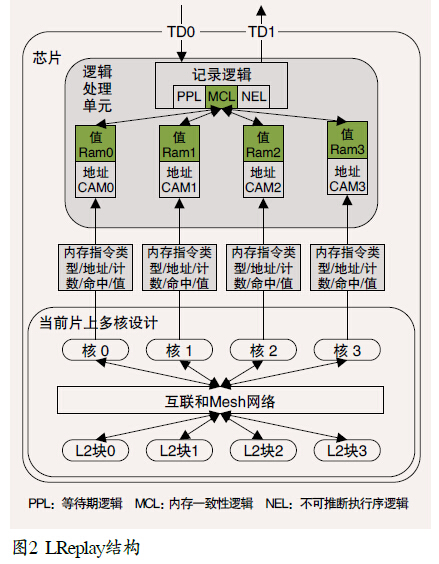
程式理論是研究程式的語義性質和程式的設計及開發方法的理論。主要包括程式語義理論、數據類型理論、程式邏輯理論、程式驗證理論、並發程式設計理論和混合程式設計理論。...
程式設計(Programming)是指設計、編制、調試程式的方法和過程。它是目標明確的智力活動。由於程式是軟體的本體,軟體的質量主要通過程式的質量來體現,在軟體研究中,...
根據錫博特(John W.Thibaut)和華爾克(Lanren walker)的觀點,程式公正性是指對於決策制定者使用政策、程式、準則以達成某一爭議或協商結果的公平知覺。程式公正性理論...
決策程式理論也稱決策過程理論。指以決策程式為研究對象,重點闡明一個完整的決策過程所包含的諸程式或階段以及諸階段的基本特徵的理論。這一理論為美國著名決策理論...
《程式設計語言理論》是2004年高等教育出版社出版的圖書,作者是陳意雲。該書主要講述了分析程式設計語言語法、操作和語義性質的一個基於λ演算系統框架。...
《程式設計語言理論基礎》是2006年電子工業出版社出版的圖書,作者是(美)米切爾。本書提出了一個框架,用於分析程式設計語言的語法、操作和語義性質,該框架基於稱為...
《實用程式設計理論》是2010年科學出版社出版的圖書,作者是EricC.R.Hehner。...... 函式理論、程式理論、程式設計語言、遞歸定義、理論設計與實現、並發和互動等內容...
編制動作程式理論是指強調中樞控制動作的理論。美國學者拉什利1917年首先提出。J A.亞當斯予以實驗驗證。動作程式指在某個相繼發出的動作開始之前,個體頭腑中已構成...
程式語言理論(PLT)是計算機科學的一個分支,涉及程式語言及其各自特徵的設計,實現,分析,表征和分類。 它屬於計算機科學學科,既依賴於並影響數學,軟體工程,語言學甚至...
程式教學,是一種使用程式教材並以個人自學形式進行的教學。程式教學主要由教學機器的發明人普萊西首創,對程式教學貢獻最大的當屬行為主義心理學家F·斯金納是美國著名...
《程式開發原理》是2006年電子工業出版社出版的圖書,作者是利斯科瓦。...... 程式開發原理內容介紹 編輯 本書由著名編程理論專家所著,是美國麻省理工學院電子工程與...
結構化程式理論也稱為伯姆-賈可皮尼理論或Böhm-Jacopini理論,是一項程式語言研究的結果,說明只要一種程式語言可以依三個方式組合其子程式及調整控制流程,每個可...
程式正確性理論(theory of program correctness)程式設計理論的一個重要組成部分.研究如何使用程式設計語言編制程式,以正確實現預定的目標.程式正確性理論提出編制正確...
程式最佳化是指改進程式,使之節省存儲空間,提高執行效率,這個過程稱為最佳化。最佳化的目標是從執行的結果程式中消除重複計算。程式最佳化的基礎:控制分析,數據流分析。程式...
可計算性理論(Computability theory)作為計算理論的一個分支,研究在不同的計算模型下哪些算法問題能夠被解決。相對應的,計算理論的另一塊主要內容,計算複雜性理論考慮...
程式的局部性原理是指程式在執行時呈現出局部性規律,即在一段時間內,整個程式的執行僅限於程式中的某一部分。相應地,執行所訪問的存儲空間也局限於某個記憶體區域...
第二,馬斯洛的需要層次理論帶有一定的機械主義色彩。一方面,他提出了人類需要發展的一般趨勢。另一方面,他又在一定程度上,把這種需要層次看成是固定的程式,看成是一...
學習理論是教育學和教育心理學的一門分支學科,描述或說明人類和動物學習的類型、過程和影響學習的各種因素的學說。學習理論是探究人類學習本質及其形成機制的心理學...
所謂科學理論是對某種經驗現象或客觀事實的科學解說和系統解釋,也是對物質世界的正確反映。它是由一系列特定的概念、原理(命題)以及對這些概念、原理(命題)的嚴密...
決策理論是把第二次世界大戰以後發展起來的系統理論、運籌學、計算機科學等綜合運用於管理決策問題,形成的一門有關決策過程、準則、類型及方法的較完整的理論體系。...
課題研究基本程式主要包括制訂課題研究方案、研究課題開題、實施課題研究和課題總結。主要介紹怎樣制定課題研究方案和怎樣實施課題研究。...
相當於文獻回顧和文獻綜述,一般論文中的理論基礎。對大學生有幫助...... 相當於文獻回顧和文獻綜述,一般論文中的理論...守法程式和行為的道德倫理規範,旨在約束追求...
契約理論”是研究在特定交易環境下來分析不同契約人之間的經濟行為與結果,往往需要通過假定條件在一定程度上簡化交易屬性,建立模型來分析並得出理論觀點。契約理論是近...
