祖暅原理

祖暅原理也稱祖氏原理，一個涉及幾何求積的著名命題。公元656年，唐代李淳風注《九章》時提到祖暅的開立圓術。祖暅在求球體積時，使用一個原理：“冪勢既同，則積不容異”。“冪”是截面積，“勢”是立體的高。意思是兩個同高的立體，如在等高處的截面積相等，則體積相等。更詳細點說就是，界於兩個平行平面之間的兩個立體，被任一平行於這兩個平面的平面所截，如果兩個截面的面積相等，則這兩個立體的體積相等。上述原理在中國被稱為祖暅原理，國外則一般稱之為卡瓦列利原理。

基本介紹

• 中文名：祖暅原理
• 別稱：祖氏原理
• 提出者：祖暅
• 提出時間：公元6世紀初
• 套用學科：數學
• 適用領域範圍：幾何求積

定義

祖暅原理，又名等冪等積定理，內容是：夾在兩個平行平面間的兩個幾何體，被平行於這兩個平行平面的任何平面所截，如果截得兩個截面的面積總相等，那么這兩個幾何體的體積相等。祖暅之《綴術》有云：“緣冪勢既同，則積不容異”。

歷史沿革

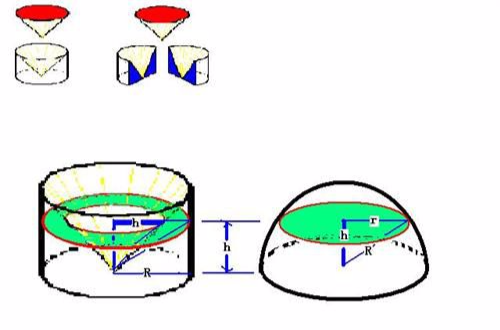
等積原理的發現起源於《九章算術》中的答案是錯誤的。他提出的難方法是取每邊為1寸的正方體棋子八枚，拼成一個邊長為2寸的正方體，在正方體內畫內切圓柱體，再在橫向畫一個同樣的內切圓柱體。這樣兩個圓柱所包含的立體共同部分像兩把上下對稱的傘，劉徽將其取名為“牟合方蓋”。（古時人稱傘為“蓋”，“牟”同侔，意即相合。）根據計算得出球體積是牟合方蓋體的體積的四分之三，可是圓柱體又比牟合方蓋大，但是《九章算術》中得出球的體積是圓柱體體積的四分之三,顯然《九章算術》中的球體積計算公式是錯誤的。劉徽認為只要求出牟合方蓋的體積，就可以求出球的體積。可怎么也找不出求導牟合方蓋體積的途徑。

兩垛歐元2分硬幣具有相同體積

祖暅沿用了劉徽的思想，利用劉徽“牟合方蓋”的理論去進行體積計算，得出“冪勢既同，則積不容異”的結論。“勢”即是高，“冪”是面積。

在西方，球體的體積計算方法雖然早已由希臘數學家阿基米德發現，但“祖暅原理”是在獨立研究的基礎上得出的，且比阿基米德的內容要豐富，涉及的問題要複雜。二者有異曲同工之妙。根據這一原理就可以求出牟合方蓋的體積，然後再導出球的體積。

這一原理主要套用於計算一些複雜幾何體的體積上面。在西方，直到17世紀，才由義大利數學家卡瓦列里（Cavalieri.B,1589-1647)發現。於1635年出版的《連續不可分幾何》中，提出了等積原理，所以西方人把它稱之為“卡瓦列里原理”。其實，他的發現要比我國的祖暅晚1100多年。

意義

我們都知道“點動成線，線動成面，面動成體”這句話，線段由點構成，點的多少表示線段的長短；面由線構成，也就是由點構成，點的多少表示面積的大小；幾何體由面構成，就是由線構成，最終也就是由點構成，點的多少也表示了體積的大小，要想讓兩個幾何體的體積相等，也就是讓構成這兩個幾何體的點的數量相同，祖暅原理就運用到了它。

兩個幾何體夾在兩平行平面中間，可以理解為這兩個幾何體平行面間的的高度相等。兩平行面之間的距離一定，若視距離為一條線段，那么這個距離上就有無數個點，過一個點，可以畫出一個平行於兩平行面的截面，若兩幾何體在被過每一點的平行截面截出的截面面積兩兩相等，則說明兩幾何體在同一高度下的每兩個截面上的點的數量相同。有無數個截面，同一高度每兩個幾何體的截面上的點的數量相同，則說明，這兩個幾何體所擁有的點數量相同，那么也就是說，它們的體積相同。所以我們可以用這種思想來理解祖暅原理。