特點
曼徹斯特編碼是二進制相移鍵控(BPSK)的一種特殊情況,其中數據控制方波載波的相位,其頻率是數據速率。曼徹斯特碼確保頻繁的線電壓轉換,與時鐘速率成正比;這有助於時鐘恢復。
編碼信號的DC分量不依賴於數據,因此不攜帶任何信息。因此,可以感應地或電容地耦合連線,允許使用網路隔離器 - 不能傳送DC分量的簡單的一對一隔離變壓器通過電隔離的介質(例如
乙太網)方便地傳送信號。
根據思科的說法,“曼徹斯特編碼引入了一些與頻率相關的難題,使其不適合以更高的數據速率使用”。
有更複雜的代碼,例如8B/10B編碼,使用較少的頻寬來實現相同的數據速率,但可能不太容忍傳送器和接收器參考時鐘中的頻率誤差和抖動。
編碼和解碼
曼徹斯特碼在每個比特周期的中間始終具有轉變,並且(取決於要傳送的信息)也具有在周期開始時的轉變。 中間位轉換的方向表示數據。 期間邊界的過渡不包含信息。 它們僅用於將信號置於正確的狀態以允許中間位轉換。
數據表示
數據表示有兩種相反的約定。
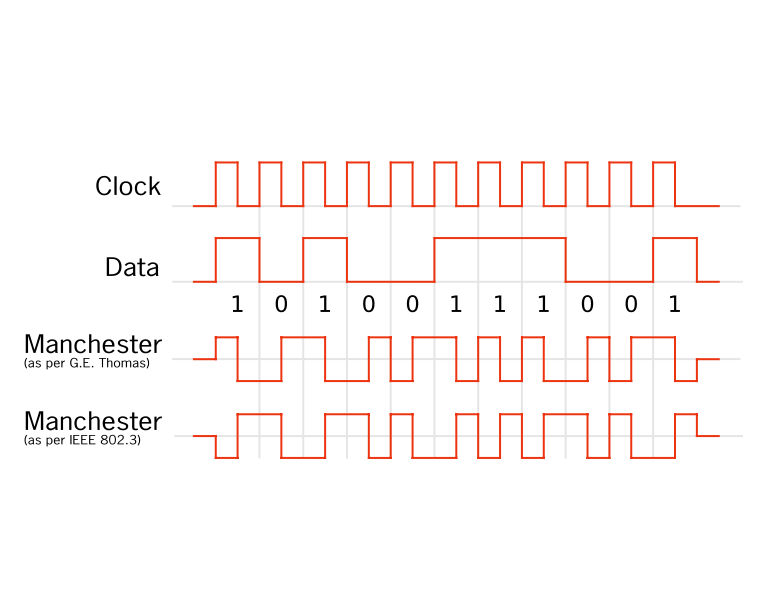
其中第一個由G. E. Thomas於1949年首次出版,隨後有許多作者(例如,Andy Tanenbaum)。[2] 它規定,對於0比特,信號電平將為低 - 高(假設數據的幅度物理編碼) - 在比特周期的前半部分具有低電平,在後半部分具有高電平。 對於1位,信號電平將為高-低。
第二個慣例也是許多作者(例如,William Stallings [3])以及IEEE 802.4(令牌匯流排)和IEEE 802.3(乙太網)標準的低速版本。 它指出邏輯0由高 - 低信號序列表示,邏輯1由低 - 高信號序列表示。
如果曼徹斯特編碼信號在通信中被反轉,則它從一個約定變換到另一個約定。 通過使用差分曼徹斯特編碼可以克服這種模糊性。
解碼
保證轉換的存在允許信號自動計時,並且還允許接收器正確對準; 接收器可以識別它是否被半個周期錯位,因為在每個比特周期期間不再總是過渡。 與更簡單的NRZ編碼方案(或參見NRZI)相比,這些優勢的價格是頻寬需求的兩倍。
編碼
編碼約定如下:
每個比特在固定時間(“周期”)中傳送。
 使用獨占或邏輯編碼數據
使用獨占或邏輯編碼數據0表示為從低到高的轉換,1表示由高到低的轉換(根據G. E. Thomas的慣例-在IEEE 802.3慣例中,反之亦然)。
表示0或1的轉變發生在周期的中點。
期間開始時的轉換是開銷,並不表示數據。
 使用獨占或邏輯編碼數據
使用獨占或邏輯編碼數據