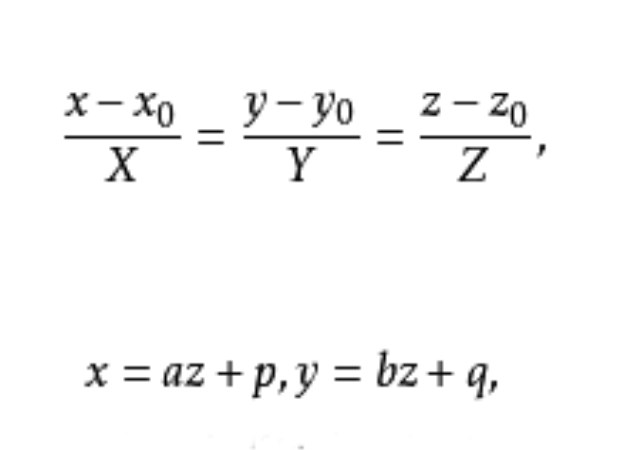直線叢

所有有三個參數的直線的集合組成直線叢。直線叢按下述意義填滿了整個空間或空間的一部分：過其中每一點都有無數多條直線屬於此集合，直線叢中經過某點的直線組成以該點為頂點的錐面。若錐面退化成為平面上的線束，則直線叢叫做線性的。

基本介紹

• 中文名：直線叢
• 外文名：bundle of straight lines
• 所屬學科：數學
• 所屬問題：空間幾何
• 別稱：直線把
• 簡介：空間滿足某些條件的直線的集合
• 分類：中心直線叢，平行直線叢

基本概念

直線叢(bundle of straight lines)亦稱直線把，是一種空間圖形，空間滿足某些條件的直線的集合。空間中通過同一個點或平行於同一條直線的全體直線的集合稱為直線叢。叢中直線共點時，此叢稱為中心直線叢，此點稱為中心直線叢的中心，叢中直線平行時，此叢稱為平行直線叢。平行直線叢無中心或說中心在無窮遠處。

直線叢的方程

中心直線把的方程

經過一個定點的空間所有直線的集合稱為一個中心直線把，它們的公共點稱為直線把的中心；平行於一條固定直線的空間所有真線的集合稱為平行直線把，以已給點 為中心的直線把方程可以寫成

其中X，Y，Z不同時為零，稱為直線把的參數；當它們取不同比值時，得直線把里不同直線，所以起作用的參數實際上只有兩個。

平行直線把的方程

平行於矢量(X，Y，Z)的平行直線把的方程也可以寫成(1)的形狀，但此時X，Y，Z為已給，改變 的值，可以得不同直線. 當然，把里每條直線上的任意兩點決定同一直線。

假設Z≠0，則平行直線把的方程可以寫成

其中 為已知，不同的數偶p, q對應 不同的直線，p，q是平行直線把(1')的參數。