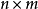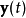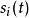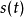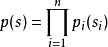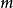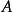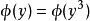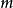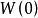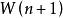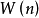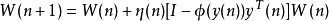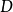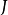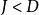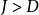簡介
從字面意思理解,信號分離就是從接收到的混合信號(典型情況下是感興趣信號+干擾+噪聲)中分別分離或恢復出原始源信號。信號分離是信號處理中的一個基本問題。各種時域濾波器、頻域濾波器、空域濾波器或碼域濾波器都可以看作是一種信號分離器,完成信號分離任務。只不過這時的“分離”僅僅是分離出需要的感興趣的信號而已,與前面講的“分離”稍有不同。由此可見,信號分離是許多信號處理共性的體現。在已知源信號和傳輸通道的先驗知識時,上述通過
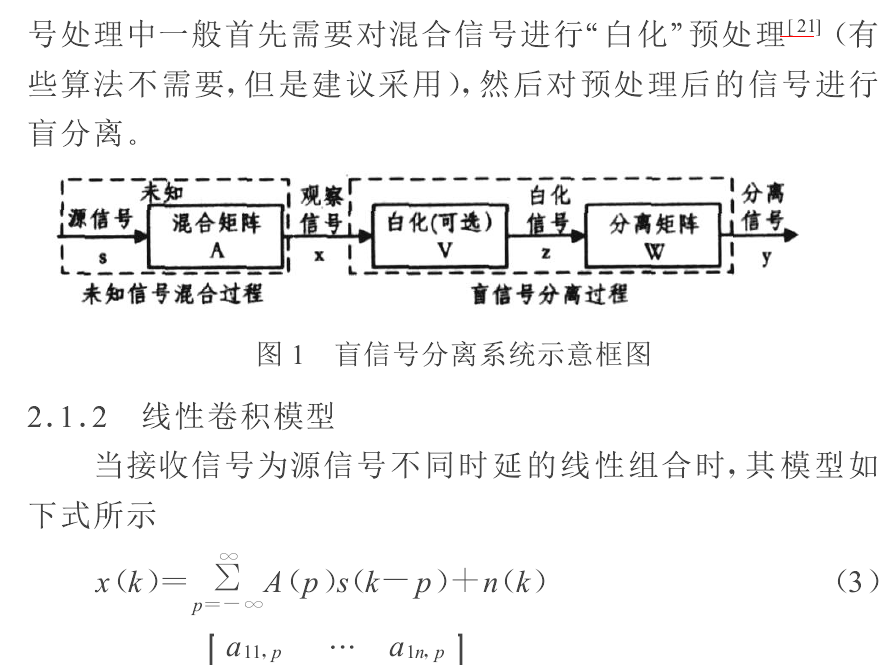
濾波的信號處理能夠在一定程度上完成信號分離的任務。然而,在沒有源信號和傳輸通道先驗信息時,通過濾波的方法根本就無法完成信號分離的任務,必須通過盲信號分離技術來解決。盲信號分離也可以稱為盲源分離(BSS,Blind Signal/Source Separation),其含義是在不知道源信號及信號混合參數的情況下,僅根據觀測到的混合信號估計源信號。
獨立分量分析(ICA,Independent Component Analysis)是為了解決盲信號分離問題而逐漸發展起來的一種新技術。盲信號分離大部分都採用獨立分量分析的方法,即將接收到的混合信號按照統計獨立的原則通過最佳化算法分解為若干獨立分量,這些獨立分量作為源信號的一種近似估計。事實上,盲信號分離中要處理的問題在數學上是欠定的,因此結果不可能只有一個,即分離結果存在兩個不確定性:分離結果排列順序不確定、分離結果幅度不確定。由於要傳送的信息往往包含在信號波形中,因此這兩個不確定性並不影響在實際中的套用。
問題基本描述
如果可以對信號混合的方式直接建模,當然是最好的方法。但是,在盲信號分離中我們並不知道,信號混合的方式,所以,只能採用統計的方法。算法做出了如下的假定:具有 m個獨立的信號源
和
個獨立的觀察量
觀察量和信號源具有如下的關係
其中
是一個
的係數矩陣,原問題變成了已知
和
的獨立性,求對
的估計問題。假定有如下公式
其中
是對
的估計,W是一個
係數矩陣,問題變成了如何有效的對矩陣W做出估計。
問題的基本假設如下:1)各源信號
均為零均值信號,實隨機變數,信號之間統計獨立。如果源信號
的機率密度為
則
的機率密度為:
。2)源信號數目
小於等於觀察信號數目
,即
。混合矩陣
是一個
的矩陣。假定
滿秩。3)源信號中只允許有一個高斯分布,當多於一個高斯分布時,源信號變得不可分。
其中
為我們需要估計的矩陣。
為步長
是一個非線性變換,比如
,實際計算時
為一個
矩陣,
為原始信號個數,
為採樣點個數。算法基本步驟為:
2)循環執行如下的步驟,直到
與
差異小於規定值
(計算矩陣差異的方法可以人為規定),有時候也人為規定疊代次數
發展
盲分離的真正進展是在20世紀80年代後期,先驅性的工作主要由Jutten和Herault在1986年完成:他們提出一種自適應的算法,完成了兩個混迭源信號的分離。後來,Jutten,Herault,Comon,Sorouchyari等人於1991年在“ SignalProcessing”上發表了關於盲源分離的3篇經典文章,標誌著盲分離問題研究獲重大進展。與此同時,L.Tong等人於1991年對盲分離問題的可辨識性進行了初步研究,直到1996年曹希仁才徹底解決了盲分離的可解性條件。1994年,Comon系統地分析了瞬時盲信號分離問題,同時明確地引入獨立分量分析(ICA)的概念,證明了只要恢復出混合信號中各個信號之間的相互獨立性,就可以完成對源信號的分離。可以說,Comon的工作實際上使得對盲信號分離算法的研究變成了對獨立分量分析的代價函式以及其最佳化算法的研究,使得以後的算法設計開始有了明確的理論依據。之後,湧現了一大批優秀的盲分離算法。A.J.Bell和T.J.Sejnowski於1995年提出了信息最大化法(Informax),T.Lee於1999年對此算法進行了改進(ExInformax);J.F.Cardoso於1996年提出了非線性PCA算法,並於1997年提出了最大似然算法。Amari於1998年提出了基於自然梯度的互信息最小算法,降低了算法計算量。Hyvarinen和Oja於1997年提出了盲分離中的定點算法FastICA,為進一步的實際套用打下了堅實基礎。進入新世紀後,隨著基本盲分離理論的逐漸成熟,越來越多的學者投入到擴展的盲分離問題的研究中,促進了含噪盲分離、欠定盲分離、卷積盲分離及非線性盲分離等的發展。在此基礎上,相關的理論總結和專著不斷湧現,進一步促進了學科的發展。“ Proceedings of IEEE” 1998年10月的論文集是盲信號處理專輯,Haykin,Hyvarinen,Cichocki等人相繼出版了盲信號分離方面的專著。
基於統計信息方法分類
自從Herault和Jutten的開創性工作以來,人們在這一領域進行了大量的研究工作,從不同角度提出了很多有效的盲分離算法。為了更好地理解並比較這些算法的原理與特點,根據一定的原則對它們進行分類是必要的。根據所用BSS的統計信息分類通常情況下,根據算法所依賴的源信號的統計信息,盲源信號分離算法可以分為如下三類:
基於資訊理論或似然估計的盲分離算法
這類算法以資訊理論為基礎,判斷信號分離的準則是分離系統輸出信號的統計獨立性最大化(互信息最小化、負熵最大化等)。這類算法除了要求源信號間相互獨立外,還要求源信號中最多只能包含一個高斯信號。Cardoso等人證明,似然估計算法等價於資訊理論算法,因此可以把似然估計算法與資訊理論算法歸到同一類中。基於資訊理論的典型算法有Amari的基於神經網路的自然梯度算法,Imformax算法等。此外,非線性算法也歸到此類。雖然非線性方法與資訊理論及似然估計方法的出發點不同,但它們在算法上很相似,而且都用非線性神經網路實現。
基於資訊理論的盲分離算法通常都是自適應線上學習算法。這類算法的不足之處在於非線性激勵函式與信號的統計分布特性(是亞高斯分布還是超高斯分布)有關。當源信號中同時存在亞高斯信號和超高斯信號時會帶來麻煩。解決的辦法有兩種,其一是自適應地估計激勵函式的類型,然後在給定的激勵函式中選擇合適的函式方法。另一種方法是對源信號的機率密度函式進行Edegworth或Gram Charlier展開,從而把非線性激勵函式表示為分離信號各階累積量的函式,並自適應地估計這些統計量。基於資訊理論的BSS方法通常具有較好的穩定性和收斂性。
基於二階統計量的盲分離算法
這類算法也稱為去相關算法。這類算法要求源信號間具有統計不相關性。此外,還要求源信號具有非白性或非平穩性。換言之,去相關算法不能分離統計獨立的、平穩的白噪聲過程(無論其機率分布如何)。去相關算法的主要優點是算法比較簡單,並具有較好的穩定性,適用於具有任何機率分布的源信號。在二階矩理論框架下,要想完整描述一個非白且非平穩的隨機過程,必須用它的二維自相關函式。從盲信號分離角度來看,源信號的非白性與非平穩性具有等價性。
基於高階統計量(HOS)的盲分離算法
在盲信號分離領域,HOS算法占有重要地位。事實上,BSS算法的早期工作是從高階統計量算法似一網路開始的。這類算法利用源信號的高階統計量的性質來分離信號。最常用的是信號四階累積量,也有人用信號的三階累積量來分離信號。這類算法除了要求源信號具有統計獨立性外,源信號中最多只能有一個高斯信號,即利用源信號的非高斯性。而對於源信號的非白特性及非平穩特性沒有做任何考慮。因此可以說,HOS算法可以用來分離任何統計獨立的非高斯信號或準確地說,不多於一個高斯信號。
獨立成分分析
統計學中,獨立成分分析或獨立分量分析(Independent components analysis,縮寫:ICA) 是一種利用統計原理進行計算的方法。它是一個線性變換。這個變換把數據或信號分離成統計獨立的非高斯的信號源的線性組合。獨立成分分析是盲信號分離(Blind source separation)的一種特例。獨立成分分析的最重要的假設就是信號源統計獨立。這個假設在大多數盲信號分離的情況中符合實際情況。即使當該假設不滿足時,仍然可以用獨立成分分析來把觀察信號統計獨立化,從而進一步分析數據的特性。獨立成分分析的經典問題是“雞尾酒會問題”(cocktail party problem)。該問題描述的是給定混合信號,如何分離出雞尾酒會中同時說話的每個人的獨立信號。當有
個信號源時,通常假設觀察信號也有
個(例如
個麥克風或者錄音機)。該假設意味著混合矩陣是個方陣,即
,其中
是輸入數據的維數,
是系統模型的維數。對於
和
的情況,學術界也分別有不同研究。獨立成分分析並不能完全恢覆信號源的具體數值,也不能解出信號源的正負符號、信號的級數或者信號的數值範圍。獨立成分分析是研究盲信號分離(blind signal separation)的一個重要方法,並且在實際中也有很多套用。