盧津猜測

俄國著名數學家盧津於1915年提出一個猜測：L²(T)中函式的傅立葉級數都是幾乎處處收斂的。

基本介紹

• 中文名：盧津猜測
• 外文名：Luzin conjecture
• 適用範圍：數理科學

簡介

盧津猜測是一元傅立葉分析中的一個重要猜測。

俄國著名數學家盧津於1915年提出一個猜測：L²(T)中函式的傅立葉級數都是幾乎處處收斂的。

結果

在盧津提出了50年後，卡爾松(Carleson,L.)於1966年發表了對盧津猜測的正面解答。他的結果是：

1、若對於某個δ>0，f·(log⁺|f|)^1+δ∈L，則對幾乎每個x，S_n(f,x)=o(log log n)。

2、若對某個ρ>1，f∈L^p，則對於幾乎每個x，S_n(f,x)=o(log log n)。

3、若f∈L²，則對幾乎每個x，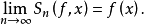

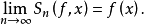
卡爾松的結果徹底解決了盧津猜測。

推廣

亨特(Hunt,R.A.)將卡爾松結果3中的f∈L²推進為f∈L^p(1<p<+∞)，這個結果一般稱為卡爾松-亨特定理。

這個成就在傅立葉級數理論的發展史上具有里程碑的意義。至此，一元傅立葉級數的理論可以說已經基本完善了。