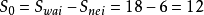皮克公式

皮克公式是奧地利數學家皮克發現的一個計算點陣中多邊形的面積公式．

基本介紹

• 中文名：皮克公式
• 外文名：Peake's theorem
• 國家：奧地利
• 提出者：數學家皮克
• 類型：一個計算點陣中多邊形的面積公式
• 別稱：畢克定理,皮克公式
• 套用學科：幾何
• 適用領域範圍 ：數學 

具體做法

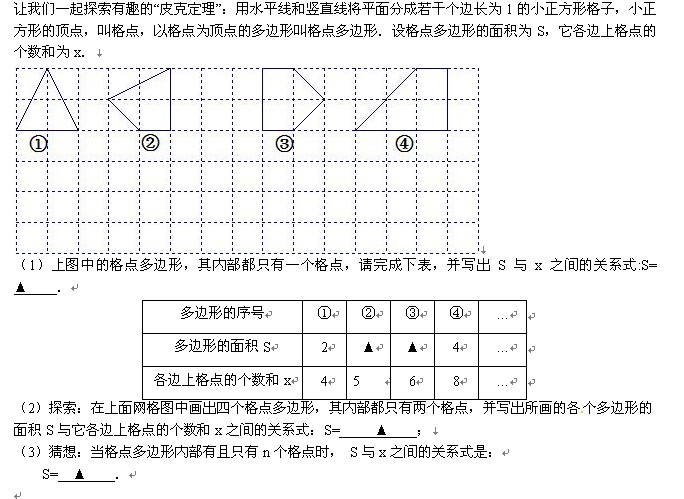
一張方格紙上，上面畫著縱橫兩組平行線，相鄰平行線之間的距離都相等，這樣兩組平行線的交點，就是所謂格點．如果取一個格點做原點O，如圖1，取通過這個格點的橫向和縱向兩直線分別做橫坐標軸Ox和縱坐標軸Oy，並取原來方格邊長做單位長，建立一個坐標系。這時前面所說的格點，顯然就是縱橫兩坐標都是整數的那些點．如圖1中的O、P、Q、M、N都是格點．由於這個緣故，我們又叫格點為整點．

s=14,n=39,S=45

一個多邊形的頂點如果全是格點，這多邊形就叫做格點多邊形。有趣的是，這種格點多邊形的面積計算起來很方便，只要數一下圖形邊線上的點的數目及圖內的點的數目，就可用公式算出．

這個公式是皮克(Pick)在1899年給出的，被稱為“皮克定理”，這是一個實用而有趣的定理．

給定頂點坐標均是整點（或正方形格點）的簡單多邊形，皮克定理說明了其面積S和內部格點數目n、邊上格點數目s的關係：

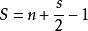
(其中n表示多邊形內部的點數,s表示多邊形邊界上的點數,S表示多邊形的面積)

皮克公式的證明

可以將邊界上的點看作是一個個圓，在多邊形邊上的圓其面積只有一半屬於這個多邊形，但多邊形角上的圓就不一樣了，將夾角的任一個邊延長，與另一條邊的夾角是外角，這角上的圓中外角部分計算面積時多算了，要除去，因多邊形的外角和是360度，所以正好是個整圓．

所以面積公式為．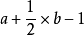

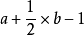
皮克公式是奧地利數學家皮克發現的一個計算點陣中多邊形的面積公式：S=a+1/2b-1其中a表示多邊形內部的點數，b表示多邊形邊界上的點數，S表示多邊形的面積，可以自己代入一下．

如果a=3，b=10，所以多邊形面積S=3+1/2*10-1=7．

易錯情形說明

如圖所示，圖是由外圈的八邊形和內圈的長方形構成的“0”形圖案，求這個“0”形的面積．

【錯誤解法一】：圖中八邊形的邊界格點數為14，長方形的邊界格點數為10，八邊形和長方形的內部格點數為0，由皮克公式可得：．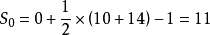

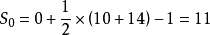
【分析】沒有正確理解內部格點數的意思 .

【正確解法】：外圈的八邊形的邊界格點數為14，內部格點數為12，所以 ；內部的長方形的邊界格點數為10，內部格點數為2，所以 ;所以 ．

【錯誤解法二】：圖中八邊形的邊界格點數為14，長方形的邊界格點數為10，整個圖形的內部格點數為2，由皮克公式可得：．

【分析】：以上錯解是沒有正確理解格點多邊形的概念。圖中的“0”其實不是一個單獨的格點多邊形，而是由兩個格點多邊形複合而成的圖形，故不能直接套用格點公式，需要分開來計算。

【正確解法】：外圈的八邊形的邊界格點數為14，內部格點數為12，所以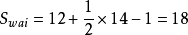；內部的長方形的邊界格點數為10，內部格點數為2，所以;

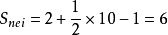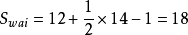
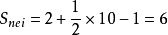
所以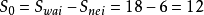．