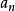發散序列(divergent sequence)是指不收斂的序列。發散的實數列分兩類,一類是有無限極限+∞或-∞的,稱為定向發散序列,其他的稱為不定向發散序列。
序列是數學分析的基本概念之一。即可用自然數編號,並按編號從小到大的次序排列的同一類數學對象。若將序列看做集合,它的元素稱為序列的項。
基本介紹
- 中文名:發散序列
- 外文名:divergent sequence
- 領域:數學
- 學科:數學分析
- 定義:不收斂的序列
- 分類:定向發散序列、不定向發散序列
概念,序列,收斂,收斂數列,函式收斂,疊代算法的斂散性,發散,發散數列,
概念
發散序列(divergent sequence)是指不收斂的序列。發散的實數列分兩類,一類是有無限極限+∞或-∞的,稱為定向發散序列,其他的稱為不定向發散序列。例如,數列{q}n≥1,當|q|<1及q=1時,分別收斂於0與1;當q≤-1時,不定向發散;當q>1時,定向發散於+∞。
序列
序列是數學分析的基本概念之一。即可用自然數編號,並按編號從小到大的次序排列的同一類數學對象。若將序列看做集合,它的元素稱為序列的項。但序列並非一般的集合,序列的項有先後次序,並且不同的項可以是相同的元素。序列可以只有有限項,稱為有限序列.不只有限項的序列稱為無窮序列,這是數學分析中通常討論的對象。序列按各項順序排列可寫為a1,a2,…,an,…,簡記為{an}或{an}n=1.排在第n位的項an稱為第n項,把n看做在自然數集N中變動時,亦把an稱為通項。序列常隨其所包含的數學對象使用不同名稱,例如:各項都是數的序列稱為數列,各項都是點的稱為點列,各項都是函式的稱為函式列。數列也可看做定義域為自然數集N或其部分Nk={1,2,…,k}的函式或映射(f∶n→an),因此亦稱整序變數。數列還常用數軸上的點列表示,所以數列與直線上的點列可以不加區分。
收斂
收斂數列
函式收斂
定義方式與數列收斂類似。柯西收斂準則:關於函式f(x)在點x0處的收斂定義。對於任意實數b>0,存在c>0,對任意x1,x2滿足0<|x1-x0|<c,0<|x2-x0|<c,有|f(x1)-f(x2)|<b。
收斂的定義方式很好的體現了數學分析的精神實質。
如果給定一個定義在區間i上的函式列,u1(x), u2(x) ,u3(x)......至un(x)....... 則由這函式列構成的表達式u1(x)+u2(x)+u3(x)+......+un(x)+......⑴稱為定義在區間i上的(函式項)無窮級數,簡稱(函式項)級數
對於每一個確定的值X0∈I,函式項級數 ⑴ 成為常數項級數u1(x0)+u2(x0)+u3(x0)+......+un(x0)+.... (2) 這個級數可能收斂也可能發散。如果級數(2)發散,就稱點x0是函式項級數(1)的發散點。函式項級數(1)的收斂點的全體稱為他的收斂域,發散點的全體稱為他的發散域對應於收斂域內任意一個數x,函式項級數稱為一收斂的常數項 級數,因而有一確定的和s。這樣,在收斂域上 ,函式項級數的和是x的函式S(x),通常稱s(x)為函式項級數的和函式,這函式的定義域就是級數的收斂域,並寫成S(x)=u1(x)+u2(x)+u3(x)+......+un(x)+......把函式項級數 ⑴ 的前n項部分和 記作Sn(x),則在收斂域上有lim n→∞Sn(x)=S(x)
記rn(x)=S(x)-Sn(x),rn(x)叫作函式級數項的餘項 (當然,只有x在收斂域上rn(x)才有意義,並有lim n→∞rn (x)=0
疊代算法的斂散性
1.全局收斂
對於任意的X0∈[a,b],由疊代式Xk+1=φ(Xk)所產生的點列收斂,即其當k→∞時,Xk的極限趨於X*,則稱Xk+1=φ(Xk)在[a,b]上收斂於X*。
2.局部收斂
若存在X*在某鄰域R={X| |X-X*|<δ},對任何的X0∈R,由Xk+1=φ(Xk)所產生的點列收斂,則稱Xk+1=φ(Xk)在R上收斂於X*。
發散
在數學分析中,與收斂(convergence)相對的概念就是發散(divergence)。發散函式的定義是:令f(x)為定義在R上的函式,如果存在實數b>0,對於任意給出的c>0,任意x1,x2滿足|x1-x2|<c,有|f(x1)-f(x2)|>b,則函式為發散函式。這條定義來自柯西收斂定則的反定則。
發散數列
①無窮大量,如數列 {en},{ (-1)nn} 等。
②無界而不是無窮大量的數列。如
{n+ (-1)nn}。
③不收斂的有界振盪數列,如 { (-1)n}。
證明數列發散,常常用到下列知識:
①數列極限的定義;
②收斂數列的有界性;
③收斂數列的子列性質。