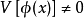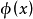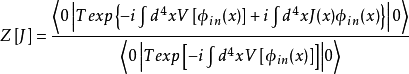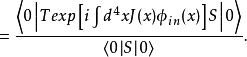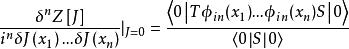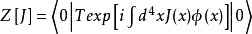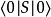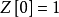生成泛函

利用路徑積分形式可以構成格林（Green）函式的生成泛函，由該生成泛函可導致格林（Green）函式。在格林函式的生成泛函的路徑積分中，出現的是經典的量、經典的場函式以及正則動量、經典的Lagrange量或經典的Hamilton量。

基本介紹

• 中文名：生成泛函
• 外文名：Generating functional
• 套用學科：量子力學術語
• 範疇：數理科學
• 涉及：格林（Green）函式
• 使用：路徑積分形式

概念

利用路徑積分形式可以構成格林（Green）函式的生成泛函，由該生成泛函可導致格林（Green）函式。在格林函式的生成泛函的路徑積分中，出現的是經典的量、經典的場函式以及正則動量、經典的Lagrange量或經典的Hamilton量。

自由場的格林函式生成泛函可寫成

上式中的是自由場算符；稱為外源函式，是數。通過對的泛函求導可以生成任意階的格林函式

這就是生成泛函的字面含義。

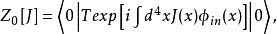
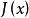
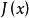
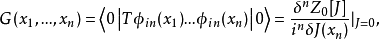
基本原理

對於存在相互作用的情形，即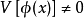，可以首先在海森堡繪景中定義生成泛函

這裡是海森堡算符。在入射繪景中它可等價地表示為

上式的泛函導數為

這就表明和兩個式子是等價的。由於的作用僅在消去展開後的真空圖形，因此我們可以略去不寫，這樣式子可簡寫為

只需要加上歸一條件，它相當於不計真空圖形的貢獻。