環行問題(circuit problem)是一種特殊路線的行程問題,指行駛路線為環狀的行程問題。有以下兩種情況:1.同時同地同向而行,求第一次相遇時間,計算公式為:第一次相遇時間=環周長÷速度差;2.同時同地背向而行,求第一次相遇時間,計算公式為:第一次相遇時間=環周長÷速度和。
基本介紹
- 中文名:環行問題
- 外文名:circuit problem
- 所屬學科:數學
- 所屬問題:算術(套用問題)
- 簡介:行駛路線為環狀的行程問題
基本介紹,說明與例題解析,相關說明,例題解析,
基本介紹
兩個物體沿環路作同向或反向運動的行程問題,叫做環行問題。它有時是相遇問題(如果兩物沿環路作反向運動),有時是追及問題(如果兩物沿環路作同向運動)。解答這類題,必須弄清兩點:①在相遇問題中,兩物從同時同地離開到相遇的路程和是環路一周的長;②在追及問題中,從同時同地同向行到追及的路程差也是環路一周的長。
說明與例題解析
相關說明
環行問題的基本特徵是路徑呈環狀或為環線的一部分。事實上,這類問題也有“相遇”與“追及”之分:
(1)若同地出發,反向而行, 則每次相遇,兩者的行程之和等於環形的周長。
 圖1
圖1(2)若同地出發,同向而行, 則每次追及,兩者的行程之差等於環行道的周長。或表為
快者的行程=慢者的行程+環形周長,
此外,若是同時出發,則相遇(或追及)時,兩者行走的時間相等。
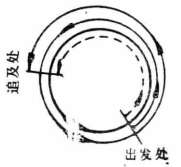 圖2
圖2例題解析
【例1】王老師和李老師在學校400米環形跑道上跑步,王老師每分鐘跑225米,李老師每分鐘跑275米。如果兩人同時伺地向相同方向起跑, 那么經過幾分鐘李老師第一次追上王老師; 如果兩人同時同地向相反方向起跑,那么經過幾分鐘兩人第一次相遇?
分析與解 兩人同時同地向相同方向起跑,李老師第一飲追.上王老師時,李老師比王老師正好多跑了一周, 即“路程差”是400米。因此,追及時間是:
400÷(275-225) = 400÷50=8(分鐘)
兩人同時同地向相反方向起跑,兩人第一次相遇時,他們跑過的路程和正好是一周,即400米。因此,相遇的時間是:
400÷(275+225)=400÷500=0.8 (分鐘)
答:如果兩人向相同方向起跑,經過8分鐘,李老師第一次追上王老師;如果兩人向相反方向起跑, 經過0.8分鐘,兩人第一次相遇。
【例2】一個湖,周長3000米。甲乙二人由湖濱同時同地出發練習跑步,甲每分鐘跑160米,乙每分鐘跑240米。如果兩人向相反方向起跑,那么經過多少分鐘兩人第一次相遇?如果兩人向相同方向起跑,那么經過多少分鐘乙第一次追上甲?
分析兩人同時同地向相反的方向起跑, 第一次相遇的時候,他們所跑過的路程和正好是湖的一周,即3000米。 用這個路程和除以兩人的速度和,就求出了第一次反向相遇的時間。
兩人同時同地向相同的方向起跑,第一次相遇的時候,即乙第一次追上甲的時候,乙正好比甲多跑湖的一用,即3000米, 這3000米就是路程差。用這個路程差除以兩人的速度差,就求出了乙第一次追上甲所用的時間。.
解: 3000÷( 160+240) =7.5(分鐘).
3000÷( 240-160) =37.5 (分鐘)
答: 如果兩人向相反的方向起跑,經過7.5分鐘兩人第一次相遇;如果兩人向相同的方向起跑,經37. 5分鐘乙第一次追上甲。
【例3】甲、乙兩人在周長400米的圓形跑道上練習跑步。已知甲每分鐘跑350米,乙每分鐘跑310米。如果兩人是同時同地出發,那么從出發到第一歡相遇要用多長時間?
分析 由於甲比乙跑得快,而跑道又是圓周形,所以兩人出發後,就好像是甲在追趕乙。當甲追上乙時,也就是兩人相遇了。由於兩人是同地出發的, 所以當甲追上乙時應是甲比乙恰好多跑了1圈,也就是多跑了400米。因為甲每分鐘比乙多跑350-310=40米,所以,400里有多少個40,便是追及時所用的時間。
解: 400÷(350- 310) =10(分鐘)
答:從出發到第一次相遇用了10分鐘。

