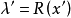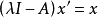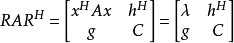瑞利商疊代法(Rayleigh quotient iteration method)是一種用瑞利商作位移的反冪法。瑞利商疊代法值得注意的是,按我們形式上敘述的誤差,收斂性是平方的,甚至是立方的(三階的)。
基本介紹
- 中文名:瑞利商疊代法
- 外文名:Rayleigh quotient iteration method
- 定義:一種用瑞利商作位移的反冪法
- 套用學科:數學術語
- 範疇:數理科學
- 涉及:反冪法
概念,基本原理,
概念
瑞利商疊代法(Rayleigh quotient iteration method)是一種用瑞利商作位移的反冪法。反冪法的收斂性和冪法本身一樣是線性的。不像冪法之處是只要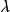 充分接近
充分接近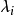 ,反冪法的收斂性係數
,反冪法的收斂性係數 可以任意小。對這一點的觀察導致在
可以任意小。對這一點的觀察導致在 中當
中當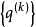 收斂到一特徵向量時,每步疊代均選取特徵值的“最佳猜測”,自適應地改變參數
收斂到一特徵向量時,每步疊代均選取特徵值的“最佳猜測”,自適應地改變參數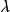 的概念。這樣,瑞利商疊代法與反冪法不同之處,在於每一疊代步
的概念。這樣,瑞利商疊代法與反冪法不同之處,在於每一疊代步 ,在
,在 中用瑞利商
中用瑞利商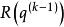 代替
代替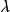 。我們用規範化的
。我們用規範化的 的殘量的
的殘量的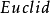 長度來度量向量
長度來度量向量 滿足特徵向量條件的偏差。具體地說,準則是
滿足特徵向量條件的偏差。具體地說,準則是
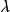
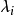


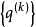
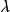


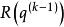
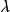


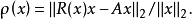
基本原理
定理:設 是按瑞利商疊代法構成的,並假定在每步疊代,對某確定的
是按瑞利商疊代法構成的,並假定在每步疊代,對某確定的 ,
,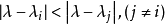 滿足,若以
滿足,若以 表示殘量的
表示殘量的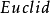 長度,即
長度,即


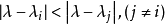

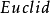


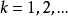
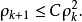
證明:設 表示一個特徵向量的估計值,假定
表示一個特徵向量的估計值,假定 ,且實部
,且實部 ,這裡
,這裡 是
是 的第一個分量,設
的第一個分量,設 是
是 變換使
變換使







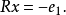







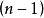
利用酋陣的性質,得到若 按
按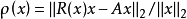 的定義則
的定義則

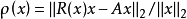
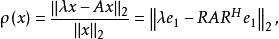
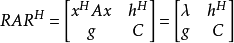

設 是由瑞利商疊代決定的,它是向量
是由瑞利商疊代決定的,它是向量 的非規範化的後繼向量,即設
的非規範化的後繼向量,即設