基本介紹
- 中文名:狄利克雷判別法
- 外文名:Dirichlet Discriminance
- 提出者:約翰·彼得·狄利克雷
- 套用學科:數學
- 適用領域範圍:積分,級數
在級數中的套用,數項級數收斂性的狄利克雷判別法,函式項級數一致收斂性的狄利克雷判別法,在積分中的套用,反常積分收斂性的狄利克雷判別法,反常含參積分一致收斂性的狄利克雷判別法,
在級數中的套用
數項級數收斂性的狄利克雷判別法
若數列  單調且趨向於0且
單調且趨向於0且 有界,則任意項數項級數
有界,則任意項數項級數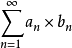 收斂
收斂


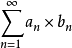
函式項級數一致收斂性的狄利克雷判別法
若函式列 對於
對於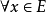 都關於n單調且在E上一致趨於0,函式項級數
都關於n單調且在E上一致趨於0,函式項級數 在E上一致有界,則函式項級數
在E上一致有界,則函式項級數 在E上一致收斂
在E上一致收斂

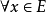


在積分中的套用
反常積分收斂性的狄利克雷判別法
無窮限反常積分收斂性的狄利克雷判別法:若 在
在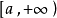 上有界,g(x)在
上有界,g(x)在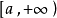 上單調,且
上單調,且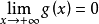 ,則無窮限反常積分
,則無窮限反常積分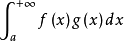 收斂
收斂

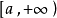
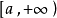
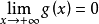
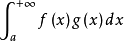
反常含參積分一致收斂性的狄利克雷判別法
若(1) 在E上一致有界,即
在E上一致有界,即 ;(2)對於每一個固定的
;(2)對於每一個固定的 ,g(x,y)是x的單調函式;(3)當
,g(x,y)是x的單調函式;(3)當 時,g(x,y)關於x在E上一致趨向於0,即
時,g(x,y)關於x在E上一致趨向於0,即 。則反常含參積分
。則反常含參積分 關於x在E上一致收斂
關於x在E上一致收斂