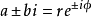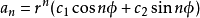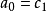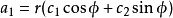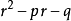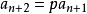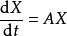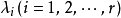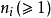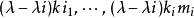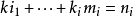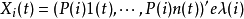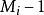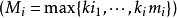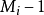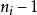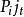基本介紹
- 中文名:特徵根法
- 外文名:Characteristic root method
- 用途:解常係數線性微分方程
- 方式:通過數列的遞推公式
- 範圍:數學
定義,利用特徵根法解方程,對微分方程:,對差分方程:,一類重特徵根對方程解的簡便解法,
定義
特徵根法是解常係數線性微分方程的一種通用方法。
特徵根法也可用於通過數列的遞推公式(即差分方程,必須為線性)求通項公式,其本質與微分方程相同。
利用特徵根法解方程
對微分方程:
設特徵方程 兩根為r1、r2。
兩根為r1、r2。

① 若實根r1不等於r2
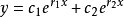
② 若實根r1=r2
③ 若有一對共軛復根a±bi
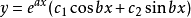
對差分方程:
1) 若特徵方程有兩個不等實根r1、r2,
則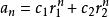
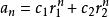
其中常數c1、c2由初始值a1=a、a2=b 唯一確定。
(1)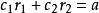
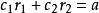
(2)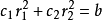
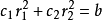
2) 若特徵方程有兩個相等實根r1=r2=r
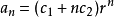
其中常數c1、c2由初始值唯一確定。
(1)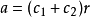
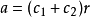
(2)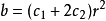
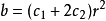
3 )若特徵方程有一對共軛復根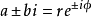 ,則有
,則有