基本介紹
- 中文名:焦耳-湯姆孫係數
- 外文名:Joule-Thomson coefficient
- 所屬學科:物理化學
- 定義:氣體經節流膨脹過程後的溫度變化與壓力變化的比值
- 符號:μJ-T
實驗








性質










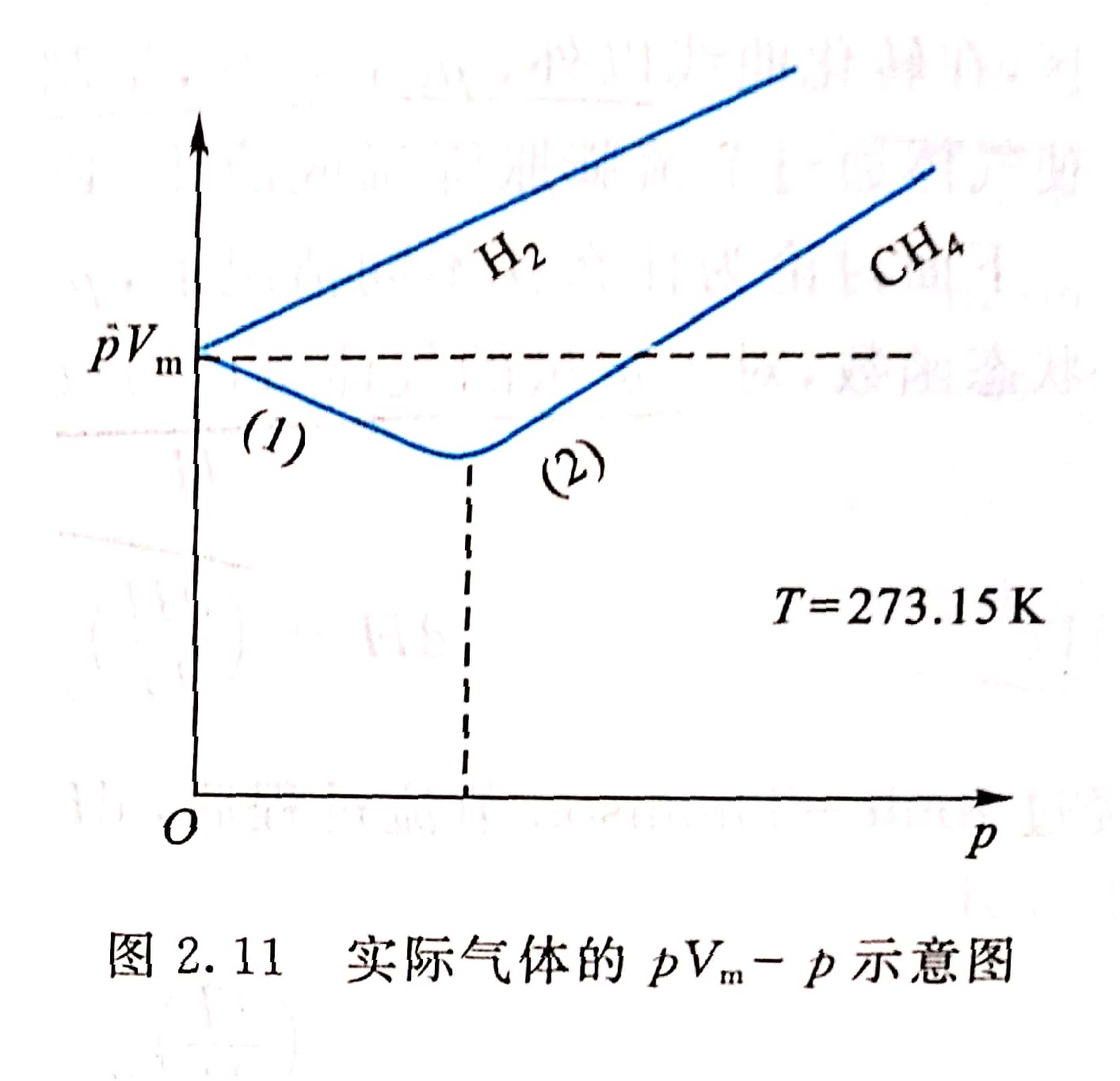
套用



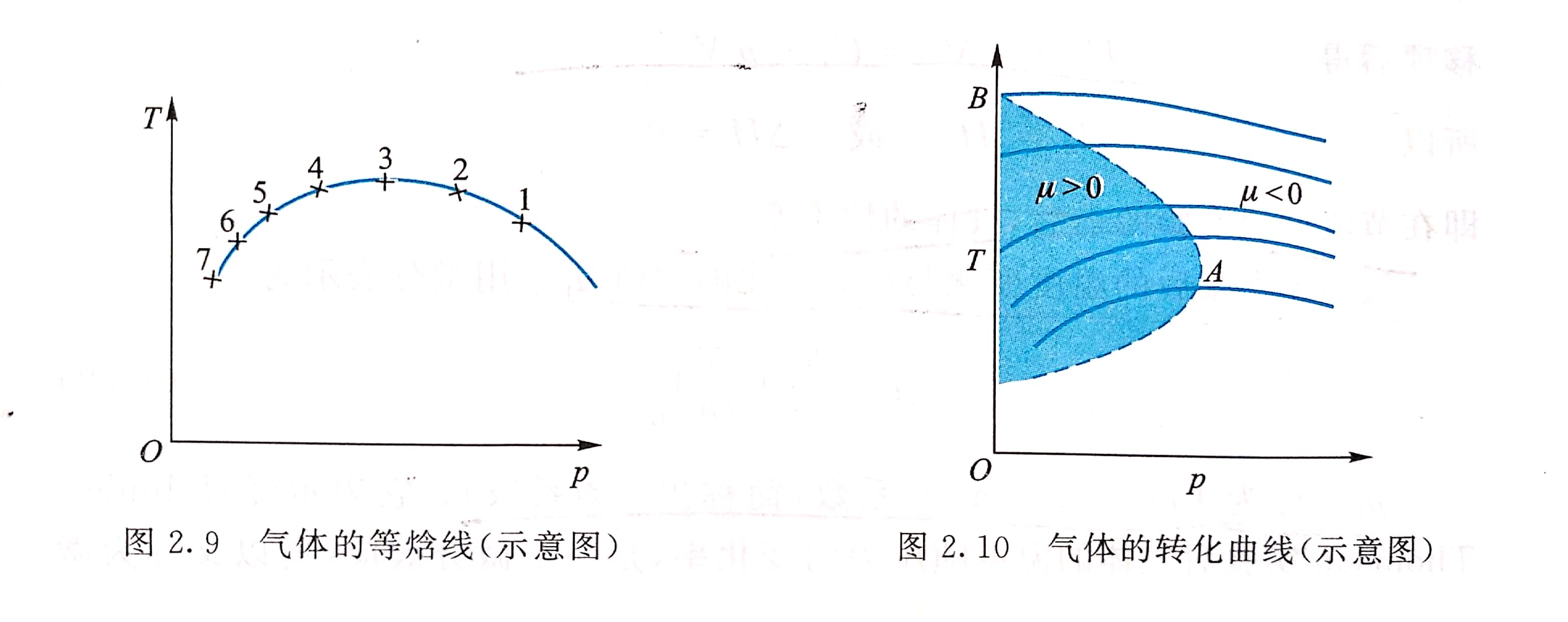
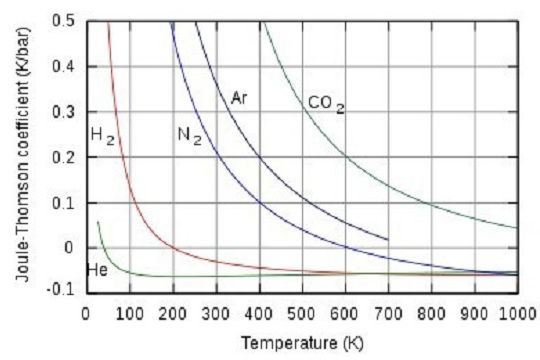
























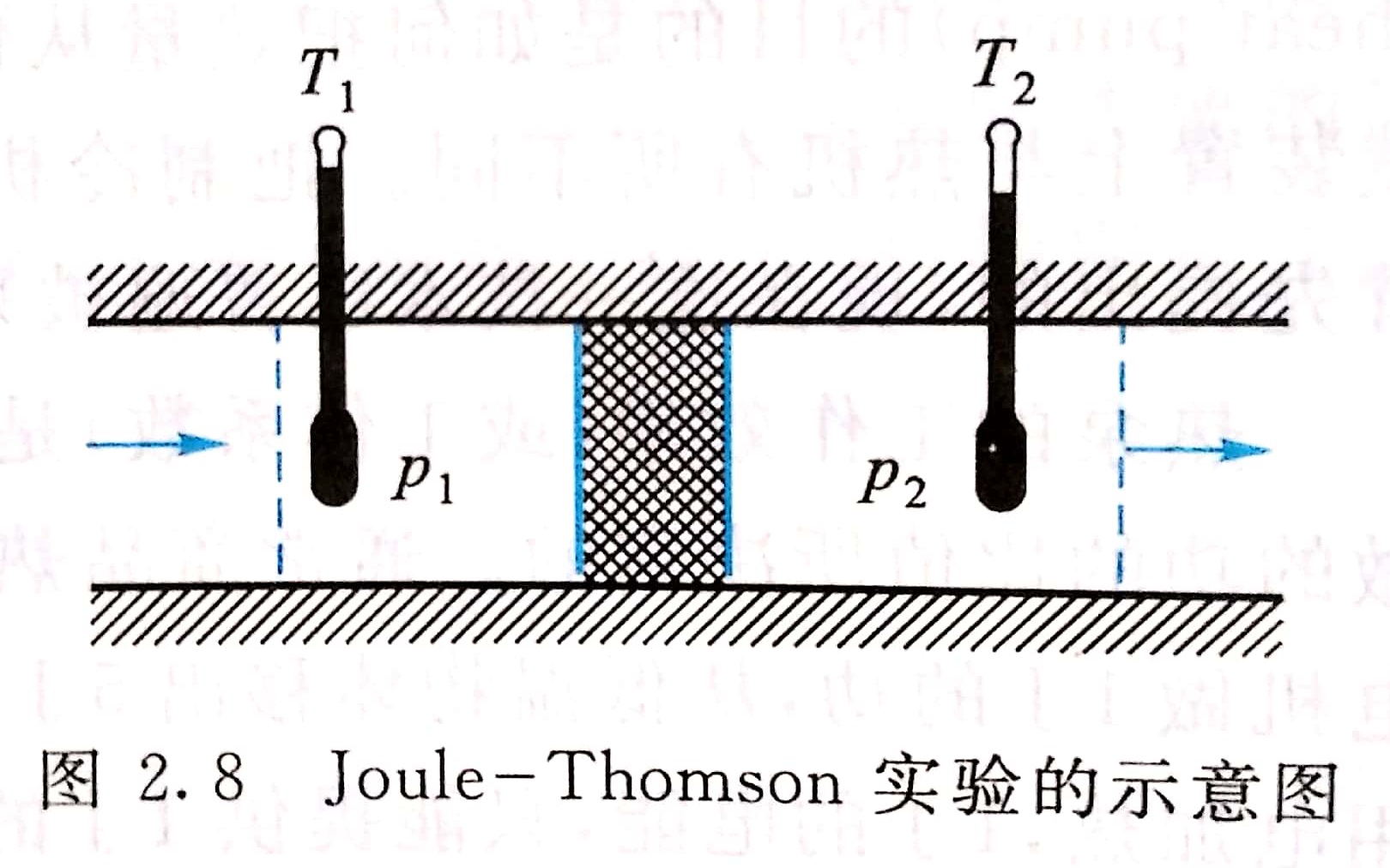
焦耳-湯姆孫係數(Joule-Thomson coefficient)是氣體經節流膨脹過程後的溫度變化與壓力變化的比值,用μJ-T表示,是系統的強度性質。實驗圖2.8為實驗裝置的示意圖。在一個圓形絕熱筒的中部,有一個用棉...
焦耳-湯姆孫效應(Joule-Thomson effect),指氣體通過多孔塞膨脹後所引起的溫度變化現象。1852年,英國物理學家J.P.焦耳和W.湯姆孫(即開爾文)為了進一步研究氣體的內能,對焦耳氣體自由膨脹實驗作了改進。原理 焦耳-湯姆孫效應是氣體在節流...
在此基礎上,他又從理論上預言了一種新的溫差電效應,即當電流在溫度不均勻的導體中流過時,導體除產生不可逆的焦耳熱之外,還要吸收或放出一定的熱量(稱為湯姆孫熱)。或者反過來,當一根金屬棒的兩端溫度不同時,金屬棒兩端會形成...
焦耳-湯姆孫效應(Joule-Thomson effect),指氣體通過多孔塞膨脹後所引起的溫度變化現象。1852年,英國物理學家J.P.焦耳和W.湯姆孫(即開爾文)為了進一步研究氣體的內能,對焦耳氣體自由膨脹實驗作了改進。 [1] ...
由焦耳-湯姆孫實驗可以發現氣體經過節流過程之後,溫度、壓強發生了改變,也就是 發生了改變,於是焦耳定義了焦耳-湯姆孫係數。並將其中改變數大於0的現象稱作製冷效應,也就是正效應 套用 經過焦耳等人的研究,臨界溫度不太低的氣體如氮氣...
所以焦耳-湯姆孫實驗(簡稱焦湯實驗)的熱力學實質是焓不改變,或者說它是一個等焓過程(isenthalpic process)。鑒於1843年,焦耳的自由膨脹實驗不夠精確,1852年焦耳和湯姆遜設計了一個節流膨脹實驗來觀察實際氣體在膨脹時所發生的溫度變化。...
歸一化的壓縮係數圖/臨界點/麥克斯韋關係/克勞修斯-克拉珀龍方程/焦耳-湯姆孫係數/潛熱方程推導/普適的熱力學方程/位力膨脹/相變/綜合題 第五章 穩定流動和不穩定流動 連續性方程/穩定流動的能量方程/亞音速噴管流動/節流熱量計/分離和...
第六節 焦耳-湯姆孫效應——實際氣體的ΔU和Δ 一、焦耳-湯姆孫實驗——節流過程 二、焦耳-湯姆孫係數 三、轉變曲線 第七節 熱化學 一、化學反應熱效應 二、反度與反應摩爾焓變 第三章熱力學第二定律與第三定律 第四章多組分系統...
為了研究節流後氣體溫度隨壓強變化的情況,通常用焦耳-湯姆孫係數 來描述,因為節流前後焓(H)不變,以 表示等焓過程中溫度隨壓強的變化率。氣體節流後壓強減小,Δp0,則μ 當氣體非常稀薄時,△T→0,可推知理想氣體節流前後溫度不變...
