無窮值邏輯悖論(infinite-valued logical para- dox)一個邏輯悖論.它是肖奚安等於1985年提出的一種無窮值邏輯悖論.
基本介紹
- 中文名:無窮值邏輯悖論
- 外文名:infinite-valued logical para- dox
簡介,套用,
簡介
無窮值邏輯悖論(infinite-valued logical para- dox)一個邏輯悖論.它是肖奚安等於1985年提出的一種無窮值邏輯悖論.關於無窮值邏輯系統與概括原則的相容性問題,在20世紀60年代初,挪威數學家斯科朗(Skolem,A. T.、)張辰中、芬斯特(Fen- sted )等作了進一步研究.在一階邏輯中,概括原則不是一條公理,而是公理模式
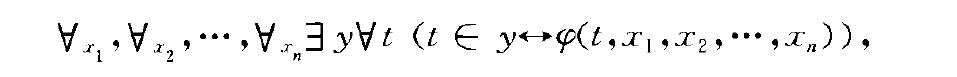
無窮值邏輯悖論
因而是無窮多條公理.通常把全體概括原則公式所構成的集記為乏。.另一方面,若對模式中之公式滬加以各種限制,就會形成各種不同的概括原則公式集,它們都是乏。的子集,分別記為乏,,乏:等.張辰中和芬斯特分別證明了武卡謝維奇連續值邏輯系統L (或帶等號的L)與上述G1 G2 G3等之間的相容性. 而對L(或Li)與乏。是否相容,則仍無結果.但應指出,即使證明了L或L,與乏。是相容的,也不表明再在萬。
套用
之外配以其他集合論公理後仍能相容.張辰中就曾證明在G2 f G3之外,再加上外延公理後,則就不再與L系統相容.但要發展整個經典數學,僅有2 `3而無其他集合論公理配套是不能實現的.要想由 L或I並完全保持概括原則而去發展整個數學,必須證明:L或I.與一個包括乏。在內、並且內涵足夠豐富的集合論系統互為相容.能否實現這一目標? 1985年,由朱梧梗、肖奚安合作完成的下述定理從反面做出了回答.任一數學系統毯,如果滿足下列條件:

滿足條件
5.自然數系統被包含在內; 則此數學系統毯必定包含悖論. 由於任一內涵足夠豐富的數學系統總能滿足上述定理中的條件2,3,4,5.因而上述結果表明:對於任何集合論系統,如果完全保持概括原則,僅僅改變與之配套的二值邏輯系統為多值(有窮或無窮值)邏輯系統,則依然要出現悖論.為區別於多值邏輯悖論而稱之為無窮值邏輯悖論.
