灰度共生矩陣

基本介紹

• 中文名：灰度共生矩陣
• 外文名：Gray-level co-occurrence matrix；GLCM
• 套用學科：通信科技

灰度共生矩陣生成

灰度直方圖是對圖像上單個像素具有某個灰度進行統計的結果，而灰度共生矩陣是對圖像上保持某距離的兩像素分別具有某灰度的狀況進行統計得到的。

取圖像(N×N)中任意一點 （x，y）及偏離它的另一點 （x+a，y+b），設該點對的灰度值為 （g1，g2）。令點（x，y） 在整個畫面上移動，則會得到各種 （g1，g2）值，設灰度值的級數為 k，則（g1，g2） 的組合共有 k 的平方種。對於整個畫面，統計出每一種 （g1，g2）值出現的次數，然後排列成一個方陣，再用（g1，g2） 出現的總次數將它們歸一化為出現的機率P（g1，g2） ，這樣的方陣稱為灰度共生矩陣。距離差分值（a，b） 取不同的數值組合，可以得到不同情況下的聯合機率矩陣。（a，b） 取值要根據紋理周期分布的特性來選擇，對於較細的紋理，選取（1，0）、（1，1）、（2，0）等小的差分值。

當 a=1，b=0時，像素對是水平的，即0度掃描；當a=0，b=1 時，像素對是垂直的，即90度掃描；當 a=1，b=1時，像素對是右對角線的，即45度掃描；當 a=-1，b=1時，像素對是左對角線，即135度掃描。

這樣，兩個象素灰度級同時發生的機率，就將 （x，y）的空間坐標轉化為“灰度對” （g1，g2）的描述，形成了灰度共生矩陣。

實驗中對灰度共生矩陣進行了如下的歸一化：

（1）

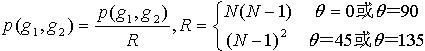
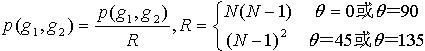
灰度共生矩陣的特徵

直覺上來說，如果圖像的是由具有相似灰度值的像素塊構成，則灰度共生矩陣的對角元素會有比較大的值；如果圖像像素灰度值在局部有變化，那么偏離對角線的元素會有比較大的值。

通常可以用一些標量來表征灰度共生矩陣的特徵，令G表示灰度共生矩陣常用的特徵有:

ASM 能量（angular second moment)

也即每個矩陣元素的平方和。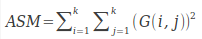

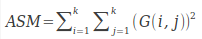
如果灰度共生矩陣中的值集中在某一塊（比如對連續灰度值圖像，值集中在對角線；對結構化的圖像，值集中在偏離對角線的位置），則ASM有較大值，若G中的值分布較均勻（如噪聲嚴重的圖像），則ASM有較小的值。

能量是灰度共生矩陣元素值的平方和，所以也稱能量，反映了圖像灰度分布均勻程度和紋理粗細度。如果共生矩陣的所有值均相等，則ASM值小；相反，如果其中一些值大而其它值小，則ASM值大。當共生矩陣中元素集中分布時，此時ASM值大。ASM值大表明一種較均一和規則變化的紋理模式。

對比度（contrast）

直接反映了某個像素值及其領域像素值的亮度的對比情況。如果偏離對角線的元素有較大值，即圖像亮度值變化很快，則CON會有較大取值，這也符合對比度的定義。其中 。反映了圖像的清晰度和紋理溝紋深淺的程度。紋理溝紋越深，其對比度越大，視覺效果越清晰；反之，對比度小，則溝紋淺，效果模糊。灰度差即對比度大的象素對越多，這個值越大。灰度公生矩陣中遠離對角線的元素值越大，CON越大。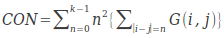

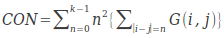
逆差矩（inverse different moment）

如果灰度共生矩陣對角元素有較大值，IDM就會取較大的值。因此連續灰度的圖像會有較大IDM值。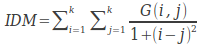

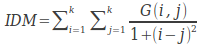
逆差矩： 反映圖像紋理的同質性，度量圖像紋理局部變化的多少。其值大則說明圖像紋理的不同區域間缺少變化，局部非常均勻。

熵（entropy）

若灰度共生矩陣值分布均勻，也即圖像近於隨機或噪聲很大，熵會有較大值。

熵是圖像所具有的信息量的度量，紋理信息也屬於圖像的信息，是一個隨機性的度量，當共生矩陣中所有元素有最大的隨機性、空間共生矩陣中所有值幾乎相等時，共生矩陣中元素分散分布時，熵較大。它表示了圖像中紋理的非均勻程度或複雜程度。

自相關（correlation）

其中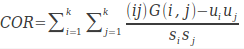

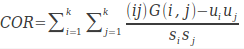
自相關反應了圖像紋理的一致性。如果圖像中有水平方向紋理，則水平方向矩陣的COR大於其餘矩陣的COR值。它度量空間灰度共生矩陣元素在行或列方向上的相似程度，因此，相關值大小反映了圖像中局部灰度相關性。當矩陣元素值均勻相等時，相關值就大;相反，如果矩陣像元值相差很大則相關值小。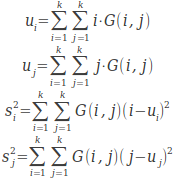

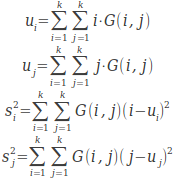
最後，可以用一個向量將以上特徵綜合在一起。例如，當距離差分值（a,b）取四種值的時候，可以綜合得到向量：

h=[ASM1, CON1, IDM1, ENT1, COR1, ..., ASM4, CON4, IDM4, ENT4, COR4]

綜合後的向量就可以看做是對圖像紋理的一種描述，可以進一步用來分類、識別、檢索等。

紋理特徵影像提取的方法

基於影像灰度共生矩陣的紋理特徵提取算法如下:

紋理特徵影像提取分為提取灰度圖像，灰度級量化，計算特徵值，紋理特徵影像的生成四部分。

提取灰度圖像

計算紋理特徵的第一步就是將多波段的影像(RGB影像)轉換為灰度圖象，求出分別代表RGB的單波段。選擇其中的一個波段進行計算紋理特徵。因為紋理特徵是一種結構特徵，即使使用不同波段的影像得到的紋理特徵都是一樣的。所以我們任意選擇了R波段作為研究的波段。

灰度級量化

在實際套用中，一幅灰度影像的灰度級一般為256級，在計算由灰度共生矩陣推導出的紋理特徵時，要求影像的灰度級遠小於256，主要是因為影像共生矩陣的計算量由影像的灰度等級和影像的大小來確定。例如:假定影像G有L個灰度級，其大小為R行C列，則運算量大約是L² * R * C，按一般情況L=256, R=512, C=512來計算，其基本運算至少要1.7 * 10十次方次。以現行微機的運算速度每秒100萬次為例，對上述一幅影像計算其灰度共生矩陣至少需要1.7 X 10³秒以上，約30分鐘。由此可見，這樣長的時間用來進行影像的識別是不太切合實際的。解決的辦法是:在儘量保持影像原形的情況下大量削減影像灰度級的取值個數和影像解析度。因此在計算空間灰度共生矩陣時，在不影響紋理特徵的前提下往往先將原影像的灰度級壓縮到較小的範圍，一般取8級或16級，以便減小共生矩陣的尺寸。

這樣進行了直方圖均衡化之後，再將灰度除以32取整之後便可以將0~255灰度級變換為0~7灰度級。

因為灰度級由256變為了8級，所以影像顏色顯得很暗淡。但是在進行紋理信息處理時對紋理特徵的影響不大。

計算特徵值

1、滑動視窗選擇

灰度共生矩陣的紋理分析方法需要選擇一定大小的滑動視窗，這裡對於每一個特徵都以5X5和7X7滑動視窗進行了計算。

2、步距的選擇

通過試驗與比較採用d=1的步距比較合適。即中心像元同與之直接相鄰的像元做運算和比較。

3、方向的選擇

通常計算灰度共生矩陣的方向取0° ,45°，90° , 135°四個方向。若是不對這四個方向綜合，則在每一方向上都可以得到多類特徵，這樣得到紋理特徵過於繁多，不利於使用。因而又可以對這四個方向的特徵值取平均值，通過比較本文取了四個方向的平均值作為最終的特徵值共生矩陣。

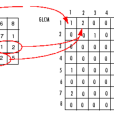
紋理特徵值的計算及生成

紋理特徵影像生成的主要思想是:用每一個小視窗形成的子影像，通過紋理特徵計算程式計算小視窗影像灰度共生矩陣和紋理特徵值，然後將代表這個視窗紋理特徵值賦值給視窗的中心點，這就完成了第一小視窗的紋理特徵計算。然後視窗被移動一個像素形成另外一個小的視窗影像，再重複計算新共生矩陣和紋理特徵值。依次類推，這樣整個圖象就會形成一個由紋理特徵值做成的一個紋理特徵值矩陣，然後將這個紋理特徵值矩陣轉換成紋理特徵影像。