漢諾塔問題

漢諾塔問題，是心理學實驗研究常用的任務之一。該問題的主要材料包括三根高度相同的柱子和一些大小及顏色不同的圓盤，三根柱子分別為起始柱A、輔助柱B及目標柱C。

基本介紹

• 中文名：漢諾塔問題
• 外文名：tower of Hanoi
• 來源：古印度漢諾塔遊戲
• 操作規則：每次只能移動一個盤子
• 目標：移動中三根桿大盤在下小盤在上
• 觀點：進行中要預先計畫和回顧性計畫

漢諾塔來源及套用

相傳在古印度聖廟中，有一種被稱為漢諾塔(Hanoi)的遊戲。該遊戲是在一塊銅板裝置上，有三根桿(編號A、B、C)，在A桿自下而上、由大到小按順序放置64個金盤(如下圖)。遊戲的目標：把A桿上的金盤全部移到C桿上，並仍保持原有順序疊好。操作規則：每次只能移動一個盤子，並且在移動過程中三根桿上都始終保持大盤在下，小盤在上，操作過程中盤子可以置於A、B、C任一桿上。

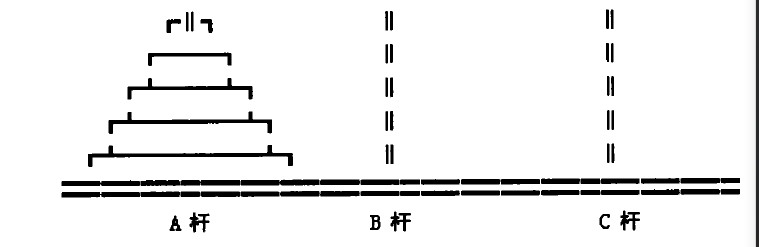漢諾塔問題圖示

分析：對於這樣一個問題，任何人都不可能直接寫出移動盤子的每一步，但我們可以利用下面的方法來解決。設移動盤子數為n，為了將這n個盤子從A桿移動到C桿，可以做以下三步：

(1)以C糟為中介，從A桿將1至n-1號盤移至B桿；

(2)將A桿中剩下的第n號盤移至C桿；

(3)以A桿為中介；從B桿將1至n-1號盤移至C桿。

這樣問題解決了，但實際操作中，只有第二步可直接完成，而第一、三步又成為移動的新問題。以上操作的實質是把移動n個盤子的問題轉化為移動n-1個盤，那一、三步如何解決？事實上，上述方法設盤子數為n, n可為任意數，該法同樣適用於移動n-1個盤。因此，依據上法，可解決n -1個盤子從A桿移到B桿(第一步)或從B桿移到C桿(第三步)問題。現在，問題由移動n個盤子的操作轉化為移動n-2個盤子的操作。依據該原理，層層遞推，即可將原問題轉化為解決移動n -2、n -3… … 3、2，直到移動1個盤的操作，而移動一個盤的操作是可以直接完成的。至此，我們的任務算作是真正完成了。而這種由繁化簡，用簡單的問題和已知的操作運算來解決複雜問題的方法，就是遞歸法。在計算機設計語言中，用遞歸法編寫的程式就是遞歸程式。

漢諾塔問題是用遞歸方法求解的一個典型問題，在實際教學中，可以在傳統教學方式的基礎上，利用計算機輔助教學進行算法的模擬演示教學，使學生更容易接受和理解遞歸算法的思想，不但能提高學生的學習興趣，而且還能取得較好的教學效果。

解決漢諾塔問題的多種觀點

計畫能力決定圓盤移動順序

目前關於漢諾塔問題解決的一個最主要的觀點認為，完成漢諾塔任務時要對圓盤的移動順序進行預先計畫和回顧性計畫活動。當問題呈現後，在開始第一步的移動之前，大多數被試都會根據設定好的目標狀態，對圓盤的移動順序進行預先計畫。以決定圓盤的移動順序，但是這種計畫能力的作用可能會受到問題難度的影響。

抑制能力參與漢諾塔問題

也有研究者認為，不是計畫能力而是抑制能力參與漢諾塔問題的解決過程。為了把更大的圓盤先放置於指定位置，必須讓較小的圓盤暫時偏離其最終應該放置的位置，但被試的自然反應總是“儘快”將圓盤移動到最終的目的地，如此反而導致錯誤，使移動步數更多，完成時間更長。

對圓盤位置的記憶

關於漢諾塔問題解決過程的爭論涉及漢諾塔任務的性質，目前臨床上常將漢諾塔任務用於腦損傷者執行功能的測查。由於執行功能存在多種表現形式，有必要對漢諾塔任務所屬的性質進行明確的歸類。另外，不同性質的記憶（空間記憶、詞語記憶等）對於漢諾塔問題解決的重要性程度有多大？在解決漢諾塔問題的過程中，對圓盤位置的記憶應該是存在的。那么這種記憶涉及的是工作記憶還是短時記憶，有研究發現漢諾塔任務與工作記憶沒有關係。但另有研究發現漢諾塔任務與空間工作記憶明顯相關，只是與詞語工作記憶關係不大。臨床上對腦損傷者或智力落後者的研究表明，空間工作記憶缺陷導致他們的漢諾塔問題成績明顯不如正常控制組。另外，漢諾塔任務與空間短時記憶的關係究竟怎樣，目前並沒有報導。