漢密爾頓迴路

漢密爾頓是由Hamiltonian音譯而來，又有人稱為哈密頓。哈密頓圖（漢密爾頓圖）（英語：Hamiltonian path，或Traceable path）是一個無向圖，由天文學家哈密頓提出，由指定的起點前往指定的終點，途中經過所有其他節點且只經過一次。在圖論中是指含有哈密頓迴路的圖，閉合的哈密頓路徑稱作哈密頓迴路（Hamiltonian cycle），含有圖中所有頂點的路徑稱作哈密頓路徑。

基本介紹

  • 中文名：漢密爾頓迴路
  • 外文名：Hamiltonian cycle
  • 基本釋義：經過圖中每個結點恰好一次的迴路
  • 歸屬學科：圖論
  • 提出者：William Rowan Hamilton
  • 方法：回溯法
由來,漢密爾頓迴路,迴路的構造,編程實現,C代碼,C++代碼,

由來

天文學家哈密頓(William Rowan Hamilton) 提出，在一個有多個城市的地圖網路中，尋找一條從給定的起點到給定的終點沿途恰好經過所有其他城市一次的路徑。
這個問題和著名的七橋問題的不同之處在於，過橋只需要確定起點，而不用確定終點。哈密頓問題尋找一條從給定的起點到給定的終點沿 途恰好經過所有其他城市一次的路徑。
漢密爾頓迴路

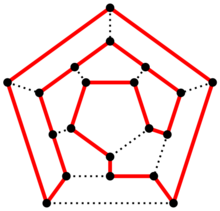
漢密爾頓迴路

哈密頓路徑問題在上世紀七十年代初，終於被證明是“NP完備”的。據說具有這樣性質的問題，難於找到一個有效的算法。實際上對於某些頂點數不到100的網路，利用現有最好的算法和計算機也需要比較荒唐的時間（比如幾百年）才能確定其是否存在一條這樣的路徑。
給定圖G，若存在一條迴路，經過圖中每個結點恰好一次，這條迴路稱作漢密爾頓迴路。
狄拉克定理：
Asimple graphwith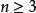
graph verticesin which eachgraph vertexhasvertex degree
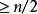has aHamiltonian cycle.
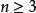
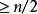
翻譯過來就是：
設一個無向圖中有 N 個節點，若所有節點的度數都大於等於 N/2，則漢密爾頓迴路一定存在。注意，“N/2” 中的除法不是整除，而是實數除法。如果 N 是偶數，當然沒有歧義；如果 N 是奇數，則該條件中的 “N/2” 等價於 “⌈N/2⌉”。

迴路的構造

證明漢密爾頓迴路存在的過程其實就是構造這條迴路的過程，分成以下幾個步驟：
  1. 任意找兩個相鄰的節點 S 和 T，在它們基礎上擴展出一條儘量長的沒有重複節點的路徑。也就是說，如果 S 與節點 v 相鄰，而且 v 不在路徑 S → T 上，則可以把該路徑變成 v → S → T，然後 v 成為新的 S。從 S 和 T 分別向兩頭擴展，直到無法擴為止，即所有與 S 或 T 相鄰的節點都在路徑 S → T 上。
  2. 若 S 與 T 相鄰，則路徑 S → T 形成了一個迴路。
  3. 若 S 與 T 不相鄰，可以構造出一個迴路。設路徑 S → T 上有 k + 2 個節點，依次為 S、 v1、 v2…… vk和 T。可以證明存在節點 vi， i ∈ [1, k)，滿足 vi與 T 相鄰，且 vi+1與 S 相鄰。證明方法也是根據鴿巢原理，既然與 S 和 T 相鄰的點都在該路徑上，它們分布的範圍只有 v1∼ vk這 k 個點， k ≤ N - 2，而 d(S) + d(T) ≥ N，那么可以想像，肯定存在一個與 S 相鄰的點 vi和一個與 T 相鄰的點 vj， 滿足 j < i。那么上面的命題也就顯然成立了。
    找到了滿足條件的節點 vi以後，就可以把原路徑變成 S → vi+1→ T → vi→ S，即形成了一個迴路。
  4. 現在我們有了一個沒有重複節點的迴路。如果它的長度為 N，則漢密爾頓迴路就找到了。
    如果迴路的長度小於 N，由於整個圖是連通的，所以在該迴路上，一定存在一點與迴路以外的點相鄰。那么從該點處把迴路斷開，就變回了一條路徑。再按照步驟 1的方法儘量擴展路徑，則一定有新的節點被加進來。接著回到步驟 2。

編程實現

C代碼

#include<stdio.h>#include<windows.h>#include<string.h>#include<stdlib.h>#define OK 1#define ERROR 0#define TRUE 1#define FALSE 0#define MAX_VER_NUM 11//頂點的最大數#define MAX_ARC_NUM 22//邊的最大數typedef char VertexType;typedef int Status;typedef struct EdgeInfo{    VertexType v1;    VertexType v2;    int weight;}EdgeInfo;typedef struct ArcBox//邊所包含的信息{    int iver;    struct ArcBox *ilink;    int jver;    struct ArcBox *jlink;    int weight;//權值    int mark;    char *info;}ArcBox;typedef struct VerBox//頂點所包含的信息{    VertexType data;//頂點值    ArcBox *firstedge;//指向鄰接點（邊所包含的信息）}VerBox;typedef struct Graph{    int vernum;//頂點總個數    int arcnum;//邊的總個數    VerBox vertexs[MAX_VER_NUM];//頂點信息}Graph;typedef struct StackData//棧中可存放的數據{    VertexType data;    int lenght;    struct StackData *pnext;}StackData;typedef struct Stack//棧用於存放已訪問過的頂點{    struct StackData *ptop;    struct StackData *pbottom;    }STNODE;typedef struct Stack_Arc//存方已訪問過的邊及頂點{    ArcBox *p[MAX_ARC_NUM];    int v_num[MAX_ARC_NUM];}SANode;int Visited[MAX_VER_NUM];//標記頂點是否被訪問過EdgeInfo Data[MAX_ARC_NUM]={{'A','B',324},{'A','J',419},{'A','K',328},{'A','D',241},{'A','C',556},{'A','F',703},{'A','G',521},{'B','G',391},{'B','H',230},{'B','I',356},{'B','J',220},{'C','F',642},{'C','E',337},{'D','F',829},{'D','K',334},{'E','F',581},{'E','G',1254},{'F','G',887},{'G','H',242},{'H','I',249},{'I','J',713},{'J','K',398}};//邊及權值int Count=0;//記可走邊的總數STNODE Stack;//存放已訪問過SANode Store_Arc_Ver;//存放弧的信息及頂點信息int LAV=-1,ALL=0;int Short_Len=1000000,Short_Load=0;//存放最斷最路經void CreateGraph(Graph **G);//創建圖int LocateVer(Graph G,VertexType v);//查找頂點v在圖中的位置void ShowAdjInfo(Graph *G);//查看鄰接點信息int FirstAdjVer(Graph *G,int v,ArcBox **u);//第一鄰接點int NextAdjVer(Graph *G,int v,int w,ArcBox **u);//下一鄰接點void NAV(ArcBox *p,int *n,int v,int w,ArcBox **u);//遞歸查找下一鄰接點void InitArcBox_mark(ArcBox *p);//初始化mark的值void DFSTraverse(Graph *G);//深度優先遍歷圖void DFST(Graph *G,int v);//剃歸深度優先遍歷void InitStack(void);//初始化棧void Push(VertexType c);//數據進棧void Pop(void);//出棧Status IsAdj(int *len,VertexType v);//判斷棧頂的點是否與A為鄰接點int main(){    Graph *G=NULL;    CreateGraph(&G);    printf("頂點的鄰接表：\n");    ShowAdjInfo(G);printf("\n\n");    printf("可走路徑結果:\n");    DFSTraverse(G);printf("\n");    printf("可走路徑總數:%d條；最短路徑為:路徑%d，長度為:%d\n\n",ALL,Short_Load,Short_Len);    return 0;}void CreateGraph(Graph **G)//創建圖{    int i,j,k,w;    char v1,v2;    ArcBox *pnew;    (*G)=(Graph *)malloc(1*sizeof(Graph));    if((*G)==NULL)    {        printf("動態記憶體分配失敗，程式終止！\n");        exit(-1);    }    (*G)->arcnum=MAX_ARC_NUM;    (*G)->vernum=MAX_VER_NUM;    for(i=0;i<(*G)->vernum;i++)    {        (*G)->vertexs[i].data='A'+i;        (*G)->vertexs[i].firstedge=NULL;    }    for(k=0;k<(*G)->arcnum;k++)    {        v1=Data[k].v1;        v2=Data[k].v2;        w=Data[k].weight;        i=LocateVer((**G),v1);        j=LocateVer((**G),v2);        if(i>=0&&j>=0)        {            pnew=(ArcBox *)malloc(1*sizeof(ArcBox));            if(pnew==NULL)            {                printf("動態記憶體分配失敗，程式終止！\n");                exit(-1);            }                        pnew->iver=i;            pnew->jver=j;            pnew->weight=w;            pnew->mark=FALSE;            pnew->ilink=(*G)->vertexs[i].firstedge;            pnew->jlink=(*G)->vertexs[j].firstedge;            (*G)->vertexs[i].firstedge=pnew;            (*G)->vertexs[j].firstedge=pnew;        }        else        {            printf("注意：*****頂點%c不存在！*****\n",i<0?v1:v2);        }    }    return;}int LocateVer(Graph G,VertexType v)//查找頂點v在圖中的位置{    int i,result=-1;    for(i=0;i<MAX_VER_NUM;i++)    {        if(G.vertexs[i].data==v)        {            result=i;            break;                }    }    return result;}void ShowAdjInfo(Graph *G)//查看鄰接點信息{    int v,w;    ArcBox *u;    for(v=0;v<G->vernum;v++)    {        printf("[%d|%c]",v,G->vertexs[v].data);        for(w=FirstAdjVer(G,v,&u);w>=0;w=NextAdjVer(G,v,w,&u))        {            printf("->[%d|%c|%d]",w,G->vertexs[w].data,u->weight);        }        InitArcBox_mark(G->vertexs[v].firstedge);        printf("\n");    }}int FirstAdjVer(Graph *G,int v,ArcBox **u)//第一鄰接點{    int w=-1;    ArcBox *p;    p=G->vertexs[v].firstedge;    (*u)=p;    if(v==p->iver)    {        w=p->jver;        p->mark=TRUE;    }    else if(v==p->jver)    {        w=p->iver;        p->mark=TRUE;    }    return w;}int NextAdjVer(Graph *G,int v,int w,ArcBox **u)//下一鄰接點{    int n=-1;    ArcBox *p;    (*u)=NULL;    p=G->vertexs[v].firstedge;    NAV(p,&n,v,w,&(*u));    return n; }void NAV(ArcBox *p,int *n,int v,int w,ArcBox **u)//遞歸查找下一鄰接點{    if(p->mark==FALSE && (p->iver==v ||p->jver==v))    {        (*u)=p;        if(p->iver==v)        {            *n=p->jver;p->mark=TRUE;        }        else if(p->jver==v)        {            *n=p->iver;p->mark=TRUE;        }        else printf("下一鄰接點數據出錯，請檢查！\n");    }    else    {        if(p->ilink!=NULL && *n==-1)        {            NAV(p->ilink,n,v,w,&(*u));        }        if(p->jlink!=NULL && *n==-1)        {            NAV(p->jlink,n,v,w,&(*u));        }    }    return;}void InitArcBox_mark(ArcBox *p)//初始化mark的值{    p->mark=FALSE;    if(p->ilink!=NULL)    {        InitArcBox_mark(p->ilink);    }    if(p->jlink!=NULL)    {        InitArcBox_mark(p->jlink);    }    return;}void DFSTraverse(Graph *G)//深度優先遍歷圖{    int v;    for(v=0;v<G->vernum;v++)    {        Visited[v]=FALSE;        InitArcBox_mark(G->vertexs[v].firstedge);    }    InitStack();    DFST(G,0);            return;}void DFST(Graph *G,int v)//剃歸深度優先遍歷{    int w=-1,flag=1,i=0,enter=1,len=0;    ArcBox *u;//鄰接點    StackData *p;    Visited[v]=TRUE;    Count++;    Push(G->vertexs[v].data);    if(Count==11&&IsAdj(&len,Stack.ptop->data)==1)     {                ALL++;        printf("路徑%-2d：",ALL);        printf("A");        p=Stack.ptop;        len=len+p->lenght;        if(Short_Len>len) Short_Load=ALL,Short_Len=len;                while(p!=Stack.pbottom)        {            printf("->%c",p->data);            p=p->pnext;        }        printf(" 總長度為：%d",len);        printf("\n");    }    for(w=FirstAdjVer(G,v,&u);w>=0;w=NextAdjVer(G,v,w,&u))    {        enter=1;        for(i=0;i<=LAV;i++)        {            if(Store_Arc_Ver.p[i]==u)            {                enter=0;                break;            }        }        if(enter==1)        {            Store_Arc_Ver.p[++LAV]=u;            Store_Arc_Ver.v_num[LAV]=v;        }        if(Visited[w]==FALSE)        {                DFST(G,w);            Visited[w]=FALSE;            Count--;            Pop();        }    }    for(LAV;Store_Arc_Ver.v_num[LAV]==v&&LAV>=0;)//還原當前頂點邊的狀態並出棧    {        Store_Arc_Ver.p[LAV]->mark=FALSE;        Store_Arc_Ver.p[LAV]=NULL;        LAV--;    }}void InitStack(void)//初始化棧{    Stack.pbottom=Stack.ptop=(StackData *)malloc(1*sizeof(StackData));    Stack.pbottom->pnext=NULL;    return;}void Push(VertexType c)//數據進棧{    StackData *pnew;    char v1,v2;    int i;    pnew=(StackData *)malloc(1*sizeof(StackData));    pnew->data=c;    if(c=='A')    {        pnew->lenght=0;    }    else    {        v1=c;        v2=Stack.ptop->data;        for(i=0;i<MAX_ARC_NUM;i++)        {            if((v1==Data[i].v1 || v1==Data[i].v2) && (v2==Data[i].v1 || v2==Data[i].v2))            {                    pnew->lenght=Stack.ptop->lenght+Data[i].weight;            }        }    }    pnew->pnext=Stack.ptop;    Stack.ptop=pnew;    return;}void Pop(void){    StackData *p;    p=Stack.ptop;    Stack.ptop=p->pnext;    free(p);}Status IsAdj(int *len,VertexType v)//判斷是棧頂的點是否與A為鄰接點{    int i;    for(i=0;i<MAX_ARC_NUM;i++)    {        if((Data[i].v1==v&&Data[i].v2=='A')||(Data[i].v1=='A'&&Data[i].v2==v))        {            *len=Data[i].weight;            return TRUE;            break;        }    }    return FALSE;}/*數據的存儲結構為鄰接多重表，解題的思路是深度優遍歷再配合回溯法，代碼僅供學習交流使用。*/

C++代碼

#include <queue>#include <cstdio>#include <set>#include <string>#include <stack>#include <cmath>#include <climits>#include <map>#include <cstdlib>#include <iostream>#include <vector>#include <algorithm>#include <cstring>#define max(a,b) (a>b?a:b)using namespace std;typedef long long(LL);typedef unsigned long long(ULL);const double eps(1e-8); char B[1<<15],*S=B,*T=B,ch;#define getc() (S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++)int aa,bb; int F(){      while(ch=getc(),(ch<'0'||ch>'9')&&ch!='-'); ch=='-'?aa=bb=0:(aa=ch-'0',bb=1);      while(ch=getc(),ch>='0'&&ch<='9')aa=aa*10+ch-'0'; return bb?aa:-aa;}#define N 100010int n,swp,cnt,z[N]; long long ans;#define swap(a,b) (swp=a,a=b,b=swp)#define abs(x) (x>0?x:-(x))#define max(a,b) (a>b?a:b)#define cmax(x) (ans<x?ans=x:1)struct P {int x,y,id,nx,ny;} p[N];bool operator<(const P&a,const P&b) {return a.nx<b.nx||a.nx==b.nx&&a.ny<b.ny;}class Graph{private:      int et,la[N],ufs[N],tot;      struct D      {            int x,y,v;            bool operator<(const D&a)const {return v<a.v;}      } d[N<<2];      struct E {int to,v,nxt;} e[N<<1];      int gf(int x) {return ufs[x]==x?x:ufs[x]=gf(ufs[x]);}      void adde(int x,int y,int v)      {            e[++et]=(E) {y,v,la[x]},la[x]=et;            e[++et]=(E) {x,v,la[y]},la[y]=et;      }public:      Graph() {et=1;}      void add(int x,int y,int v) {d[++tot]=(D) {x,y,v};}      void make()      {            std::sort(d+1,d+1+tot);            for(int i=1; i<=n; i++)ufs[i]=i; cnt=n;            for(int i=1,x,y; i<=tot; i++)                  if((x=gf(d[i].x))!=(y=gf(d[i].y)))                  {                        ufs[x]=y,cnt--,ans+=d[i].v,                                            adde(d[i].x,d[i].y,d[i].v);                  }      }} G;struct D {int x,n;} d[N];bool operator<(const D&a,const D&b) {return a.x<b.x;}#define dis(i,j) (abs(p[i].x-p[j].x)+abs(p[i].y-p[j].y))void ins(int i){      for(int t=p[i].ny; t<=cnt; t+=t&-t)            if(z[t]==0||p[z[t]].x+p[z[t]].y<p[i].x+p[i].y)z[t]=i;}int query(int i){      int f=0;      for(int t=p[i].ny; t>0; t-=t&-t)            if(z[t]&&(f==0||p[z[t]].x+p[z[t]].y>p[f].x+p[f].y))f=z[t];      return f;}void work(){      for(int i=1; i<=n; i++)p[i].nx=p[i].x-p[i].y,p[i].ny=p[i].y;      std::sort(p+1,p+1+n);      for(int i=1; i<=n; i++)d[i]=(D) {p[i].ny,i};      std::sort(d+1,d+1+n); d[n+1].x=d[n].x; cnt=1;      for(int i=1; i<=n; i++)      {            p[d[i].n].ny=cnt;            if(d[i].x!=d[i+1].x)cnt++;      }      memset(z,0,sizeof(z));      for(int i=1,j; i<=n; ins(i++))            if(j=query(i))G.add(p[i].id,p[j].id,dis(i,j));}int main(){      n=F();      for(int i=1; i<=n; i++)p[i]=(P) {F(),F(),i}; work();      for(int i=1; i<=n; i++)swap(p[i].x,p[i].y); work();      for(int i=1; i<=n; i++)p[i].y=-p[i].y; work();      for(int i=1; i<=n; i++)swap(p[i].x,p[i].y); work(); G.make();      printf("%lld\n",ans);}/** this code is made by crazyacking* Verdict: Accepted* Submission Date: 2015-09-11-15.31* Time: 0MS* Memory: 137KB*/

相關詞條

熱門詞條

聯絡我們