基本介紹
- 中文名：彼得森圖
- 外文名：Petersen graph
- 提出者：彼得森(Petersen,1839-1910)
- 提出時間：1898年
- 套用學科：數學
- 適用領域範圍：圖論
- 特性：常作為反例圖出現
提出者,特殊性,對稱性,基本參數,三部圖,補圖,其他性質,推廣,
提出者
彼得森是一位出色的名教師。他講課遇到推理困難時，總是說：“這是顯而易見的”，並讓學生自己查閱他的著作。同時，他是一位有經驗的作家，論述問題很形象，講究形式的優雅。
1891年，彼得森發表了一篇奠定他圖論歷史地位的長達28頁的論文。這篇文章被公認是第一篇包含圖論基本結論的文章。同時也是第一次在文章中使用“圖”術語。
1898年，彼得森又發表了一篇只有3頁的論文，在這篇文章中，為舉反例構造了著名的彼得森圖。
特殊性
Petersen圖G滿足哈密爾頓圖的通常性質ω(G-S)≤|S|，即圖G去除一些頂點（這些定點的集合為S）後形成的新圖分支數少於或等於S中元素的個數。但同時它並不是哈密爾頓圖，這導致了它不同尋常的地位，從而常常作為反例出現在圖論之中。
哈密爾頓圖性質ω(G-S)≤|S|的證明：取出H圖（哈密爾頓圖的簡稱）的H圈C，G-S只比C-S多邊，因而ω(G-S)≤ω(C-S)是顯然的，而由於C是迴路，刪去k個頂點最多產生k個分支，ω(C-S)≤|S|也成立，得證。
對稱性
基本參數
- 頂點數v=10
- 邊數e=15
- 分支數ω=1
- 各頂點的度為d(v)=3，因而它是三正則圖（頂點的度只與之相連的邊的數目）
- 圍長C=5（一個圖的圍長是指它所包含的最短圈的周長，由於通過枚舉可以發現Petersen圖中無三圈與四圈，其圍長為5）
- 直徑d=2（一個圖兩點間的距離指其間最短路的長，而它的直徑則指全圖中最大的距離）
三部圖
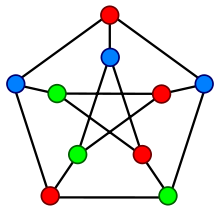
如圖，Petersen圖的頂點可以如此分為三個部分，使各個部分中的點互不相連。因此，Petersen圖是三部圖。
補圖
設G = (V,E)是一個簡單圖，G*= (V,E*)是與圖G相對應的完全圖。 定義圖G的補圖H= (V,E') ，其中： E'= E*\E。當然圖G與圖H互為補圖。而Petersen圖的補圖6正則圖！這是非常漂亮的性質，而其正確性可以由它是3正則圖直接導出。
其他性質
推廣
Desargues圖—Petersen圖的推廣
如圖
Desargues圖
Desargues圖