設A是n階矩陣, 若r（A） = n, 則稱A為滿秩矩陣。但滿秩不局限於n階矩陣。
若矩陣秩等於行數，稱為行滿秩；若矩陣秩等於列數，稱為列滿秩。既是行滿秩又是列滿秩則為n階矩陣即n階方陣。行滿秩矩陣就是行向量線性無關，列滿秩矩陣就是列向量線性無關；所以如果是方陣,行滿秩矩陣與列滿秩矩陣是等價的。
基本介紹
- 中文名：滿秩矩陣
- 外文名：non-singular matrix
- 別稱：矩陣
- 提出者：凱利
- 重要性：判斷矩陣是否可逆的充分必要條件
- 記為：R（A）
矩陣的秩,單位陣,
矩陣的秩
定義1:用初等行變換將矩陣A化為階梯形矩陣, 則矩陣中非零行的個數就定義為這個矩陣的秩, 記為r（A），根據這個定義, 矩陣的秩可以通過初等行變換求得。需要注意的是, 矩陣的階梯形並不是唯一的, 但是階梯形中非零行的個數總是一致的。
定義2:在
中，若
（1）有某個r階子式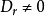
;
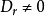
（2）所有r+1階子式
（如果有r+1階子式的話）
稱A的秩為r，記作R（A)=r。規定：R（O)=0.
對，若R（A)=m，稱A為行滿秩矩陣；
若R（A)=n，稱A為列滿秩矩陣。
若R（A)<n，稱A為降秩矩陣（不可逆矩陣，奇異矩陣）。
滿秩矩陣是一個很重要的概念, 它是判斷一個矩陣是否可逆的充分必要條件。
單位陣
單位陣是單位矩陣的簡稱，它指的是對角線上都是1，其餘元素皆為0的矩陣。
在矩陣的乘法中,有一種矩陣起著特殊的作用，如同數的乘法中的1，我們稱這種矩陣為單位矩陣，簡稱單位陣。它是個方陣，除左上角到右下角的對角線(稱為主對角線)上的元素均為1以外全都為0。
可用將係數矩陣轉化成單位矩陣的方法解線性方程組。
