同一模型在大氣條件下的臨界雷諾數和在風洞氣流中的臨界雷諾數之比。
基本介紹
- 中文名：湍流度因子
- 外文名：Turbulence factor
- 領域：空氣動力學
- 計算方法：大氣和風洞條件下的臨界Re之比
- 學科：流體力學
- 相似名詞：湍流度
簡介,臨界雷諾數,定義,由來,原理,雷諾試驗,
簡介
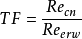
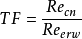
同一模型在大氣條件下的臨界雷諾數和在風洞氣流中的臨界雷諾數之比，就叫作湍流度因子。即 
分子為大氣條件下的臨界雷諾數，分母為風洞氣流中的臨界雷諾數。
臨界雷諾數
定義
臨界雷諾數（critical Reynold’s number），當流體在管道中、板面上或具有一定形狀的物體表面上流過時，流體的一部或全部會隨條件的變化而由層流轉變為湍流，此時，摩擦係數、阻力係數等會發生顯著的變化。轉變點處的雷諾數即為臨界雷諾數。
由來
雷諾根據大量的實驗發現，由層流轉變為湍流的轉變過程非常複雜，不僅與流速v有關，而且還與流體密度ρ、粘滯係數μ和物體的某一特徵長度d例如管道直徑、機翼寬度、處於流體中的球體半徑等）有關。他綜合以上各方面的因素，引入一個無量綱的量ρvd/μ，後人把這無量綱的參數命名為“雷諾數”。流體的流動狀態由雷諾數決定，雷諾數小時作層流，雷諾數大時作湍流。換言之：流速越大，流過物體表面距離愈長，密度越大，層流邊界層便愈容易變成湍流邊界層。相反，粘性越大，流動起來便愈穩定，愈不容易變成湍流邊界層。流體由層流向湍流過渡的雷諾數，叫做臨界雷諾數，記作Re。
對於圓形管道引入 Re= pvd/μ。實驗表明，流體通過圓形管道時其臨界雷諾數為Re≈2000—2600；通過光滑的同心環狀縫隙時 Re=1100；而在滑閥閥口處，Re=260。
原理
雷諾通過圓管內的黏性流動實驗，發現一定條件下層流轉化為湍流的控制因素是雷諾數Re。由層流轉變為湍流的雷諾數稱為臨界雷諾數Reα。它不是一個固定的值，依賴於外部擾動的大小。如果所受的擾動小，Reα較大；反之，Reα較小。
實驗證明：Reα的下界約為2000，當Re<2000時，黏性力的抑制作用占優，不管外部擾動有多大，管內流動總保持穩定的層流狀態。當Re>2000而小於某一上界時，流動出現不穩定，在管內(離入口較遠處)，層流與湍流共存。當Re大於某上界時，黏性力已無法抑制擾動的增長，導致流動失穩，成為隨機的脈動運動，即轉變為完全發展的湍流。
從空間角度看，即使Re>Reα，在管內中心沿流動方向也存在著層流區、過渡區和湍流區，這是因為管道入口處擾動由小到大的增長需要一定的時間，即需要經歷一定的空間區域，湍流不是在某一空間位置突然發生的。
雷諾試驗
早在19世紀初，就有人注意到流體在不同的流速範圍內，斷面流速分布和能量損失規律等都不相同。1883年，英國物理學家雷諾通過實驗揭示了流體的兩種不同的流動狀態。
在水箱A的側面開一個小孔，接一根進口為流線型管嘴的玻璃管丁，在玻璃管丁的末端裝有節門C以調節流量。在水箱的上部裝有儲存帶色液體的容器，用一根細管將帶色液體引至玻璃管丁的入口，其流量用節門E調節。
實驗前，先把水注入水箱中，利用溢流槽保持水位不變。然後，稍稍打開節門c，使水緩慢地由玻璃管T流出。打開節門E，使帶色液體也流入玻璃管中。此時在玻璃管丁內看到一條細線形狀的帶色液線。這說明液體質點在作互不干擾、各自成層的平行直線流動。
將節門C逐漸開大，玻璃管T內水的流速也逐漸增大，起初帶色液線並無變化，直到管內流速增大到某一數值時，帶色液線開始顫動和分散。
隨著玻璃管T內流速的繼續增大，達一定數值後，帶色液線不再連續，而是立即分散並與水相混淆。這說明液體質點已相互摻混，在雜亂無章地向前運動。
通過雷諾實驗人們認識到，流動存在以下三種不同的狀態。第一種，流體的質點之間互不摻混、質點的運動軌跡為有條不紊的層狀流動，稱為層流；第二種，流體的質點之間相互摻混、質點的運動軌跡為雜亂無章的流動，稱為紊流；第三種，表現為層流到紊流或紊流到層流的過渡，稱為過渡狀態。隨流速的變化而呈現不同的流動狀態，是自然界中一切流體運動普遍存在的物理現象。
