湍流剪應力又可稱為湍流切應力。流體作湍流運動時所產生的應力,除了粘性應力外尚有附加的應力,包括法向附加應力和切向附加應力,這些附加的應力都是湍流所特有的。所以湍流應力可以分為切應力和正應力,而其中切應力又可以分為雷諾切應力和黏性切應力兩部分。
基本介紹
- 中文名:湍流剪應力
- 外文名:turbulent shear stress
- 學科:流體力學
- 組成:雷諾切應力、粘性切應力
基本概念
公式推導









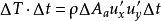



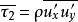


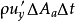




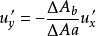












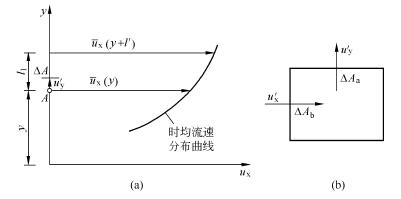 圖1
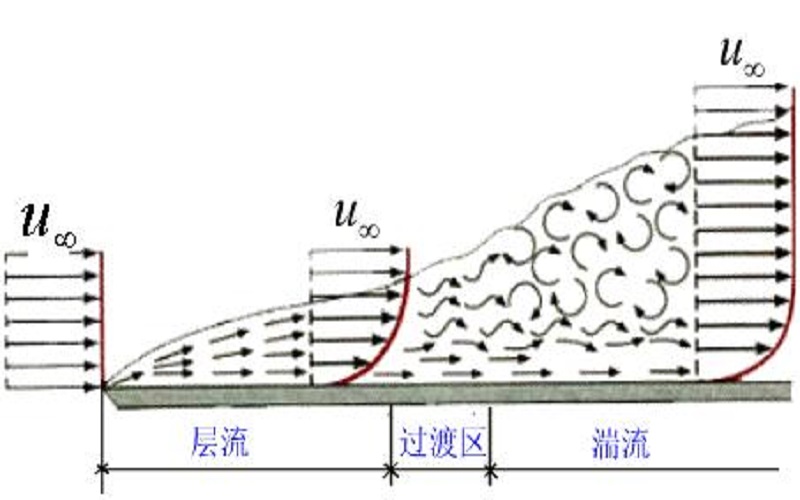
圖1混合長度理論




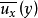


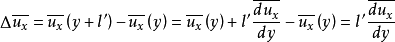

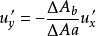


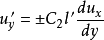




湍流剪應力又可稱為湍流切應力。流體作湍流運動時所產生的應力,除了粘性應力外尚有附加的應力,包括法向附加應力和切向附加應力,這些附加的應力都是湍流所特有的。所以湍流應力可以分為切應力和正應力,而其中切應力又可以分為雷諾切應力和黏性切應力兩部分。









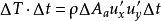



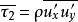


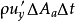




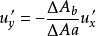












 圖1
圖1





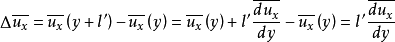

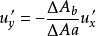


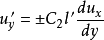




湍流剪應力又可稱為湍流切應力。流體作湍流運動時所產生的應力,除了粘性應力外尚有附加的應力,包括法向附加應力和切向附加應力,這些附加的應力都是湍流所特有的。...
湍流切應力是與湍流動量輸送相伴隨的表現應力,是由湍流強度漲落引起的。以u’,v’,w’分別表示直角坐標三個方向的湍流速度,各湍流速度分量乘積的平均值再乘上空氣...
湍流應力,又稱雷諾應力,是指雷諾方程中脈動動量交換所引起的附加應力。它包括附加法向應力和附加剪應力。...
·湍流粘度考慮到了湍流剪應力的傳播。·模型常量不同。這些改進使得SST k-ω模型比標準k-ω模型在廣泛的流動領域中有更高的精度和可信度。...
層流過渡為湍流的主要原因是不穩定性。在多數情況下,剪下流中的擾動會逐漸增長,...它用湍能K和湍能耗散率ε兩個量來描寫湍流的脈動場,用下式表示雷諾應力:...
但測量剪下湍流並不比測量均勻各向同性湍流複雜。剪下湍流的實驗測量,除了上述均勻各向同性湍流中測量的那些參量外,一個最重要的參量是雷諾應力。此外還有渦粘性係數、...
2.5.1具有恆定應力的流動 2.5.2非零質量傳遞 2.5.3混合長度逼近 2.5.4混合長度理論的局限 習題 第3章湍流動力學 3.1平均流的動能理論 3.1.1單純剪下流動 3.1...
套用PDF模型計算的平面混合層流流動、平面尾流、平面射流和軸對稱射流四種剪下流動的擴展率、平均速度的分布和Reynolds應力的計算值與試驗值吻合較好。用這種方法對湍流...
大氣湍流運動中伴隨著能量、動量、物質的傳遞和交換,傳遞速度遠遠大於層流,因此湍流中的擴散、剪下應力和能量傳遞也大得多。所以,大氣湍流對飛行器的飛行性能、結構...
4.3.5快速畸變近似的雷諾應力再分配項4.4剪下湍流中的擬序運動4.4.1自由剪下湍流中的擬序結構4.4.2湍流邊界層的擬序結構4.5擬序特性的檢測...
均值流動方程;自由剪下流;湍流運動尺度;壁流;(第二部分)模型和仿真:模型和仿真引入;直接數值模擬;湍流渦粘度模型;雷諾應力及其相關模型;PDF方法;大渦模擬;(第三...
4.3.5快速畸變近似的雷諾應力再分配項4.4剪下湍流中的擬序運動4.4.1自由剪下湍流中的擬序結構4.4.2湍流邊界層的擬序結構4.5擬序特性的檢測...
第2章介紹湍流的統計學描述,重點是引入封閉雷諾應力的湍流黏性概念,推導了平均...第4章中介紹自由剪下流動,包括自由射流和尾流。第5章是關於渦動力學,渦量是...
因此,對於定常平面湍性射流,以下湍流邊界層方程組(見湍流理論)近似成立。式中ū、vˉ為x、y方向的平均速度;ρ為流體密度;τ為湍流剪應力。為求解以上方程組,...
研究發現,幾乎所有近壁區的雷諾應力是在猝發過程中產生的,伴隨著猝發現象,常...Rashidi和Banerjee沿用固壁湍流邊界層相干結構的研究思路,對受剪下但無波動的水...
④在很強的局部剪應力處,渦旋破裂,產生三維湍流脈動,⑤在湍流速度脈動很大的地方,產生許多湍流班點;固⑥許多湍流斑點聯合在一起,發展成為完全發展了的湍流邊界層。...
後者還能使自由剪下流中的非擬序小尺度結構變少。較早的研究結果還表明,在壁湍流中加入高分子聚合物後,能使壁面切應力減小,最近的研究探明這一結果與擬序結構的...
十九世紀後期,Boussinesq提出用渦粘性係數的方法來模擬湍流流動,通過渦粘度將雷諾應力和平均流場聯繫起來,渦粘係數的數值用實驗方法確定。渦粘係數類模型由於其簡便性,...
·湍流粘度考慮到了湍流剪應力的傳波。 ·模型常量不同 這些改進使得SST k-ω模型比標準k-ω模型在在廣泛的流動領域中有更高的精度和可信度。 中文名 超級系統...
因此,對於定常平面湍性射流,以下湍流邊界層方程組(見湍流理論)近似成立:式中ū、尌為x、y方向的平均速度;ρ為流體密度;τ為湍流剪應力。為求解以上方程組,首先...
在湍流中,緊靠固體邊界附近的地方,因脈動流速很小,由脈動流速產生的附加切應力也很小,而流速梯度卻很大,所以粘滯切應力起主導作用,其流態基本上屬於層流。因此湍流...
