液體自由表面上此起彼伏的波浪運動。液體自由表面是指江河、湖泊、海洋以及開口容器中的液體等接觸大氣的液面。
基本介紹
- 中文名:液體自由表面波
- 外文名:free surface waves in liquid
- 特點:自由表面的曲率很小
簡介,性質,分類,小振幅波,斯托克斯波,孤立波,參考文獻,
簡介
液體自由表面波和其他機械運動波一樣,是質點振動在介質中的傳播。
靜止的液體自由表面是水平的,但在極輕微的局部擾動下,水平狀態就會被破壞,出現波浪運動(圖1)。液體自由表面一離開平衡狀態,液體的重力和表面張力等就會發揮回復力的作用,促其返回平衡位置,從而形成液體質點的振動和振動的傳播(即波)。起回復力作用的液體的重力和表面張力在液體自由表面波動中所起的作用往 圖1 液體自由表面波
圖1 液體自由表面波
 圖1 液體自由表面波
圖1 液體自由表面波往不是同等的。液體的表面張力又稱毛細力,其大小取決於液體及其表面的曲率。如果自由表面波的波長比波高大得多,在波動過程中自由表面的曲率便很小,因而表面張力也很小。在這種情況下,可以忽略表面張力的影響,只考慮重力的作用,這種液體自由表面波稱為重力波。反之,若波長極短,波動過程中自由表面的曲率很大,因而表面張力也很大。在這種情況下,可以忽略液體重力的影響,只考慮表面張力的作用,這種液體自由表面波稱為毛細波或漣波,其波長在1~2厘米之間。微風吹皺的一湖春水就是毛細波的一例(圖2)。
性質
液體自由表面波具有非常明顯的“自由表面層”性質,波動中液體質點的運動隨著所處自由表面下的深度的增加而急劇衰減。在自由水面下深度為一個波長處,液體質點的振幅減小到只有自由水面上質點振幅的1/535。因此,液體底面邊界對液體自由表面波的影響有三種情況。第一種情況是,液體深度h相對彼長λ足夠大,即h/λ》1,底面邊界對自由表面波動幾乎不發生任何影響。這種沒有底面邊界影響,相當於無限深情況的液體自由表面波稱為無限液深自由表面波。由於自然界液體自由表面波大都發生在自由水面上,故無限液深自由表面波常簡稱深水波。第二種情況是,λ和h為同一量級,底面邊界條件對自由表面波動性質產生明顯影響。這種液體自由表面波稱為有限液深自由表面波或有限水深波。第三種情況是,h/λ《1,底面邊界條件使自由表面波動性質發生根本變化。這種液體自由表面波稱為無限淺自由表面波或淺水波。淺水波的波長比其波高大得多,故又常稱為長波或淺水長波。 圖2 湖面的毛細波
圖2 湖面的毛細波
 圖2 湖面的毛細波
圖2 湖面的毛細波液體自由表面波的要素有頻率、周期、波長、波高、波幅、波數和波速(又稱相速)等(圖3)。波的頻率f和周期T就是波動過程中液體質點在平衡位置振動的頻率和周期。波長λ是在一個振動周期內波傳播的距離,即 在波傳播方向上,相鄰兩同相位點之間的距離。波高H是波峰至其前一個波谷的垂直距離。波輻a是波峰至靜止液面的垂直距離,或靜止液面至波谷的垂直距離。波高是波幅的兩倍。波數是在波傳播方向上單位長度內波的個數,它是波長的倒數,但通常稱2π除以波長為波數,即k=2π/λ。波速c又稱相速,是波沿傳播方向的移動速度。 圖3 液體自由表面波的要素示意圖
圖3 液體自由表面波的要素示意圖
 圖3 液體自由表面波的要素示意圖
圖3 液體自由表面波的要素示意圖液體自由表面波的振動圓頻率ω和波數k(或波長λ)之間有確定的關係,稱為頻散關係。液體自由表面波的頻散關係決定於液體自由表面上的運動學和動力學邊界條件。因此,不同的頻散關係就是液體自由表面上不同波動特徵的描述。
一般情況下,液體自由表面波的波速同波長有關,不同波長的波具有不同的傳播速度。但也有波速與波長無關的液體自由表面波,例如淺水波。波速取決於波長的波稱為彌散波,波速同波長無關的波稱為非彌散波。
分類
若波長比波高大得多,則自由表面的曲率很小,表面張力也很小,可忽略其作用,只考慮重力,這種液體自由表面波稱為重力波。反之,若波長極短,則自由表面曲率很大,表面張力也很大,可忽略重力作用,只考慮表面張力,這種波稱為毛細波或漣波,其波長在1~2厘米之間。微風吹皺的一湖春水就是毛細波的一例。液體自由表面波的要素同波的要素基本一致。波速依賴于波長的稱彌散波,如深水重力波、毛細波等;波速與波長無關的稱非彌散波,如淺水重力波。小振幅波的波速為,式中h為液深;σ為表面張力;ρ為液體密度;k為波數;g為重力加速度。對毛細波,只考慮表面張力作用。在有限振幅波中,斯托克斯波的波速為c=(g/k),式中a為波幅。孤立波的波速 ,式中h為無波時靜止液面的水深。許多單個波組成的波群的傳播速度稱為群速。若干波幅和周期都很接近的進行波疊加後形成波列,波列的包絡稱為波包。波包包絡許多單個波,又稱波群(圖1),波群的波長比其中單個波的波長大得多 。群速cg同波速c的關係由瑞利公式給出:,式中λ為波長。彌散波的群速不等於波速,例如深水重力波的群速等於其波速的一半;毛細波的群速為波速的3/2倍。非彌散波的群速同波速相等。群速也是波能量的傳播速度。
小振幅波
振輻與波長相比為一小量的液體自由表面波。由於a/λ是一小量,小振幅波中液體質點的運動速度分量、自由表面位移和波的傾角也都是小量,從而使運動基本方程和邊界條件都線性化,且流動有勢。因此,小振幅波即為液體自由表面的線性波。小振幅波有規則波和疊加波兩種模型。 圖 4 小振幅進行波
圖 4 小振幅進行波
 圖 4 小振幅進行波
圖 4 小振幅進行波規則波
液體質點作簡諧振動的簡諧波,其波形為正,餘弦函式,是液體自由表面小振幅波的基本形式。依照傅立葉定理,任何一般形式的小振幅波都可由基本的規則波疊加而成,且其中的每一種基本波(即傅立葉分量)都是獨立地進行傳播的,因此規則波的性質反映一般小振幅波的性質。規則波有進行波和駐波,下面分別闡述它們的平面形式。
①平面進行波:波形為:z=a sin (kx-ωt),式中z為液體自由表面離開其平衡位置的位移;a為波幅;k為波數;ω=2πf為振動圓頻率。如圖4所示,進行波保持波形不變,沿x正向以波速c=ω/k行進,進行波的頻散關係為:
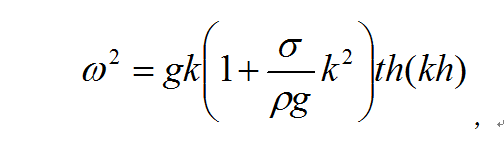
式中h為液體深度;σ為液體的表面張力。因此,進行波的波速為:

對毛細波(漣波),只考慮表面張力的作用,波速為:
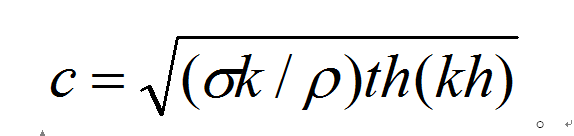
對重力波,只考慮液體重力的作用,波速為:
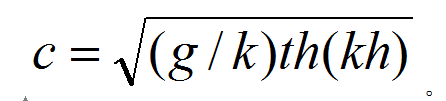
無限水深時,h→∞,th(kh)→1,重力波的波速為:

淺水時kh《1,th(kh)≈kh重力波的波速為:  。
。

由此可見,淺水重力波的波速與波長無關,所以是一種非彌散波。
在無限深液體自由表面進行波中,液體質點圍繞各自平衡位置作圓周運動,其半徑在自由表面上為波幅a,隨質點所處自由面下的深度而按指數律遞減(圖5a)。有限水深和淺水中的進行波,其流體質點運動的軌跡為具有水平長軸的橢圓(圖5b)。橢圓的長軸和短軸都隨質點所處自由面下的深度而遞減,短軸比長軸遞減得更快;短軸在自由表面上等於波幅,遞減至底面時為零,水愈淺,橢圓愈扁。

平面進行波在一個波長內的總能量為常值ρga2λ/2。總能量由動能和勢能兩部分組成,它們各占一半,始終保持不變。進行波主要發生在傳播不受阻擋和沒有其他干擾的開闊水域。
②平面駐波:波形為:
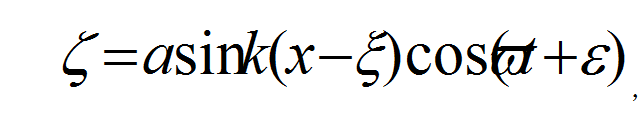
式中為振動的初始相位;ε為波的起始相位。kζ駐波可由兩個完全相同但在相反方向傳播的進行波疊加得到。駐波有周期性變化的波幅和固定不動的波節點。駐波的質點運動軌跡是直線,即液體質點在各自的平衡位置作直線振動,軌跡直線在波峰和波谷處是垂直於水平的,隨著向波節點靠近,軌跡直線與水平的夾角逐漸變小,至波節點處變為零,成為水平(圖6)。質點振動的振幅,在液體自由面上等於波幅a,隨質點所處自由面下深度的增加而迅速遞減。 圖6 平面駐波的質點運動軌跡
圖6 平面駐波的質點運動軌跡
 圖6 平面駐波的質點運動軌跡
圖6 平面駐波的質點運動軌跡駐波在一個波長內的總能量為常值ρga2λ/4,但動能和勢能周期性地相互交換。駐波主要發生在受限制水域,如湖泊、水庫,港灣以及開口容器中的液體自由表面上。
疊加波
若干個波幅和周期都很接近的規則進行波疊加後形成的波列。疊加波波列的包絡稱為波包。波包的波長比波列中單個波的波長大得多。波包包絡著許多單個波,組成波的群落,所以波包又稱波群(圖67)。波群的移動速度稱為群速,記作cg,群速與波速之間的關係由瑞利公式給出:
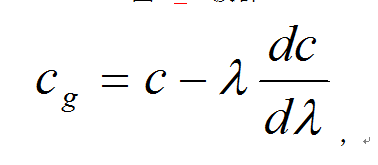
式中λ為波長。彌散波的波速依賴于波長,因而群速不等於波速。例如深水重力波,其波速 ,而群速只是它的一半。非彌散波的波速與波長無關,因而群速與波速相等。例如淺水重力波,其波速
,而群速只是它的一半。非彌散波的波速與波長無關,因而群速與波速相等。例如淺水重力波,其波速 (h為水深),而群速等於波速,即cg=c。一般形式的線性波都由不同周期的規則波疊加而成,因此波列運動、波群和群速是一般形式線性波的波動現象和波的要素。群速也是波能的傳遞速度。
(h為水深),而群速等於波速,即cg=c。一般形式的線性波都由不同周期的規則波疊加而成,因此波列運動、波群和群速是一般形式線性波的波動現象和波的要素。群速也是波能的傳遞速度。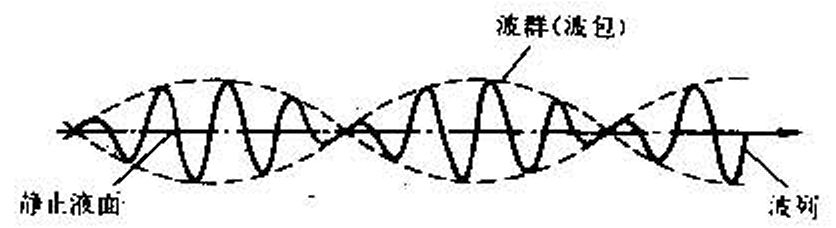 圖7 波群
圖7 波群


 圖7 波群
圖7 波群擺線波
波形為擺線的液體自由表面波(圖78),是F. J. von格斯特納於1802年在數學上首先提出的,所以又稱格斯特納波。擺線波建立在理想不可壓縮液體運動方程精確求解的基礎上,基本方程和邊界條件都沒有作線性化處理,所以它是一種有限振幅的非線性波。格斯特納考慮二維無限液深情形,採用拉格朗日變數描述流體運動。在擺線波的波動中,平衡位置為(a,b)的流體質點在時刻t的位置為: 圖8 擺線波
圖8 擺線波
 圖8 擺線波
圖8 擺線波x=a+Rekbsin k(a-ct)
y=b-Rekbcos k(a-ct),
式中k為波數;c=ω/k為波速。因此,流體質點以其平衡位置為中心作半徑為Rekb的圓周運動,這個半徑隨平衡位置所在自由面下的深度按指數律遞減。在液體自由表面上,b=0,液體質點運動軌跡的豐徑為R,因而擺線波波形的參量方程為:
x=a+R sin k(a-ct),
y=-R cos k(a-ct)。
上式是半徑為R的圓沿Ox軸滾動時圓周上一點的軌跡(擺線)方程,擺線波因此得名。
擺線波是液體自由表面的一種有旋波,其渦量為:
Q=-2ωk2R2e2kb/(1-k2R2e2kb)。
斯托克斯波
一種無旋的非線性液體自由表面波,是G. G. 斯托克斯於1847年最先用攝動法在無限深液體重力波中求解出來的,因而得名。流動無旋的液體自由表面波的非線性影響來自液體自由表面的邊界條件。對這種邊界條件,可以振幅a與波長λ的比值δ為小參量,把邊界條件的非線性方程展開為逐級近似的方程,然後再逐級求解。事實上,小振幅線性波就是這裡的零級近似。這樣逐級近似求得的高階近似非線性液體自由表面波即為斯托克斯波。在液體深度為無限的情形下,斯托克斯重力波的波形ζ為: 圖9斯托克斯波
圖9斯托克斯波
 圖9斯托克斯波
圖9斯托克斯波
這裡所取的坐標係為隨波行進的動坐標系。圖89給出的是ka=1/2,精確到k4a4項的斯托克斯波的波形圖。這種波的波峰較尖,波谷較平坦。
斯托克斯波明顯反映出液體自由表面波的非線性影響。首先與線性波不同,斯托克斯波的波速受波幅影響。其次,線性波可以疊加,且被疊加的各分量波各自獨立地進行傳播;而斯托克斯波的各分量波之間相互干擾並產生新的分量波,在共振條件下,新波將不斷從原型波中吸收能量而使自己的波幅不斷增長,故存在不穩定性。理論和實驗都證明,在深度為h的有限水深情況下,當kh>1.363時,二維周期波在相近頻率干擾波的干擾下,是不穩定的。
孤立波
一種非線性淺水波,又稱孤波,其波形為在平衡液面上的單個波峰,波峰前後沒有其他液面起伏的傳播(圖910)。孤立波在傳播過程中保持固定的波形,理論波長為無限大。其波形為:
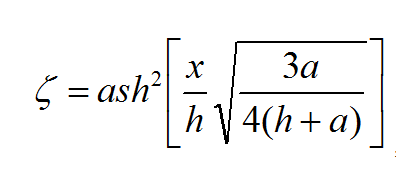
僅有一個孤立波峰的非線性波(圖4)。 孤立波在傳播過程中保持固定波形,理論波長為無限大。其波形為,式中h為平衡時的水深;坐標系Oxy是隨波行進的。當a≈h時,波形不穩定並產生碎波。孤立波是一種實際存在的波,已被用作一種環境條件來計算海洋結構物的載荷和回響。淺水航道中大平底船的運動或河流中來流速度的突然變化都會產生孤立波。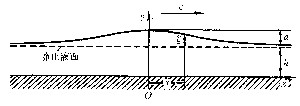 圖4 孤立波
圖4 孤立波
 圖4 孤立波
圖4 孤立波式中h為平衡時的水深1坐標系Oxy是隨波行進的。波速 。當孤立波的波幅近似等於水深時,波形就不穩定並產生斷波。淺水航道中大平底船的運動或河流中來流速度的突然變化常會產生孤立波。
。當孤立波的波幅近似等於水深時,波形就不穩定並產生斷波。淺水航道中大平底船的運動或河流中來流速度的突然變化常會產生孤立波。

參考文獻
1.易家訓著,章克本、張滌明、陳啟強、蔡崇喜譯:《流體力學》,高等教育出版社,北京,1983。(Chia-Shan Yih, Fluid Mecha-nics,McGraw-Hill,New York,1969.)
2.M. J. Lighthill,Waves in Fluid,Cambridge Univ. Press,Cambridge,1978.
3.G. B. Whitham,Linear and Nonlinear Waves,John Wiley & Sons,New York,1974.

