波特圖是線性非時變系統的傳遞函式對頻率的半對數坐標圖,利用波特圖可以看出系統的頻率回響。又稱幅頻回響和相頻回響曲線圖。
基本介紹
- 中文名:波特圖
- 外文名:Bode plots
- 領域:電路
- 對數尺度:log scale
簡介
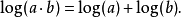
在系統穩定性的套用
相關符號定義
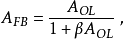
- AFB是考慮反饋時的放大器增益(閉環增益)
- β是反饋係數
- AOL是不考慮反饋時的放大器增益(開環增益)。
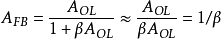
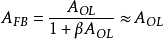
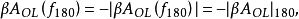

增益裕度
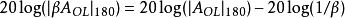
相位裕度
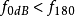

波特圖是線性非時變系統的傳遞函式對頻率的半對數坐標圖,利用波特圖可以看出系統的頻率回響。又稱幅頻回響和相頻回響曲線圖。
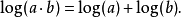
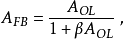
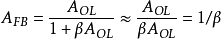
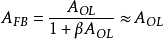
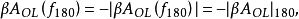

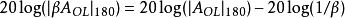
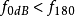
波特圖是線性非時變系統的傳遞函式對頻率的半對數坐標圖,利用波特圖可以看出系統的頻率回響。又稱幅頻回響和相頻回響曲線圖。...
波特圖是線性非時變系統的傳遞函式對頻率的半對數坐標圖,其橫軸頻率以對數尺度(log scale)表示,利用波特圖可以看出系統的頻率回響。又稱幅頻回響和相頻回響曲線圖...
畢翠克絲·波特(BeatrixPotter,1866~1943)生於倫敦一個富有的家庭,是英國著名的兒童讀物作家。在英國乃至世界卡通史上,有一個著名的兔子的形象——彼得兔。...
瓊泰·波特,美國籃球運動員,效力於密蘇里大學籃球隊。 ...... 瓊泰·波特,美國籃球運動員,效力於密蘇里大學籃球隊。 [1-2] 參考資料 1. Jontay Porter .nbadra...
阿不思·西弗勒斯·波特(Albus Severus Potter),於2005年9月至2006年8月間出生。阿不思是哈利·波特(阿不思的父親,全名哈利·波特)和金妮·波特(阿不思的母親...
巴爾塔沙·波特,中國史籍記載為“出海王”,17世紀荷蘭荷蘭東印度公司海軍提督。...... 巴爾塔沙·波特,中國史籍記載為“出海王”,17世紀荷蘭荷蘭東印度公司海軍提督。...
麥可·波特(Michael E.Porter,1947—)他是哈佛商學院的大學教授(大學教授,University Professor,是哈佛大學的最高榮譽,麥可·波特是該校歷史上第四位獲得此項...
詹姆·波特(James Potter)是英國作家喬安·凱瑟琳·羅琳(J·K·羅琳)的兒童奇幻小說《哈利·波特》系列中的人物,是哈利·波特的父親。入學後與小天狼星·布萊克,...
比爾·波特,美國當代作家、翻譯家和著名漢學家。服兵役以後去加州大學讀人類學,1970年~1972年,比爾在哥倫比亞大學讀人類學博士。從1972年用獎學金從美國去台灣佛光...
克里斯·波特,1960年8月23日出生於加拿大安大略省多倫多,美國男演員。2011年,出演電影《勇士的心》。...
