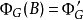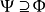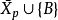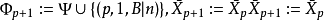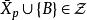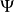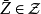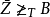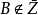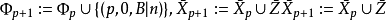基本介紹
- 中文名:波斯納–羅賓遜定理
- 外文名:Posner–Robinson Theorem
- 分類:遞歸論、數學定理
- 領域:數理科學
定理,證明,
定理
設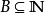 不可計算,則存在集合
不可計算,則存在集合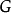 令
令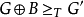 。
。
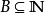
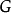
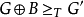
證明
這一定理證明如下:令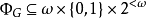 ,則
,則 可以看作是一個函式
可以看作是一個函式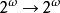 ,具體定義為
,具體定義為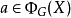 若且唯若存在
若且唯若存在 使
使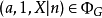 。 然而
。 然而 的每一個元素都可以用自然數編碼,因此
的每一個元素都可以用自然數編碼,因此 本身也是
本身也是 的元素,因此可以求出其圖靈跳躍。顯然
的元素,因此可以求出其圖靈跳躍。顯然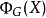 可以從
可以從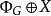 計算得出,因此假若存在
計算得出,因此假若存在 使得
使得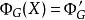 ,則
,則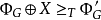 。因此證明過程只需給出構造
。因此證明過程只需給出構造 的方法。
的方法。
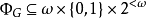

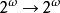
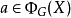

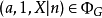



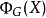
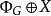

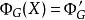
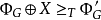

為了構造 ,我們給出一對序列
,我們給出一對序列 ,其中:
,其中:


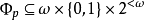
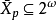
該序列滿足以下條件,若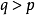 則有:
則有:
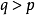
1、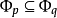 且
且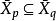
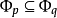
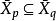
2、若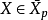 則
則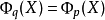
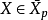
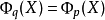
3、若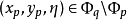 且
且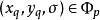 則
則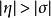
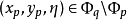
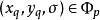
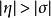
首先令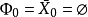 ,其後對任何
,其後對任何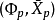 如下構造
如下構造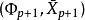 :令
:令 為編號為
為編號為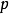 的
的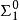 公式(詳見算數階層)。為了讓
公式(詳見算數階層)。為了讓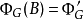 ,我們需要讓
,我們需要讓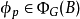 若且唯若
若且唯若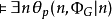 。這是一個自引用的定義:我們需要在
。這是一個自引用的定義:我們需要在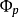 中加入B枝上的元素以表達
中加入B枝上的元素以表達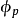 為真或為假,但是若
為真或為假,但是若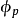 需要為假,則加入元素的過程本身卻可能將其變為真,這便是需要
需要為假,則加入元素的過程本身卻可能將其變為真,這便是需要 以控制之後可能加入的元素的原因。考慮以下兩種情況:
以控制之後可能加入的元素的原因。考慮以下兩種情況:
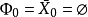
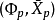
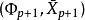

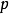
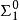
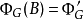
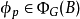
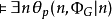
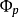
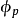
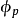

2、若不存在如上所述的集合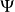 ,則對任何滿足條件3的集合
,則對任何滿足條件3的集合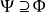 均有
均有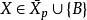 使
使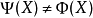 。定義類
。定義類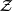 如下:
如下:
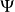
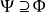
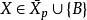
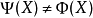
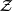
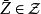
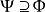
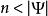
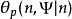
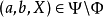
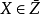
根據以上描述的序列,顯然 滿足
滿足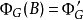 ,故定理得證。這一證明方式叫做隈部–斯萊曼力迫法。
,故定理得證。這一證明方式叫做隈部–斯萊曼力迫法。