氣體分子的平均自由程是由氣體分子相繼兩次碰撞間所走路程的平均值。在氣體分子的碰撞理論的剛球模型中,認為分子只在碰撞的一剎那發生相互作用,而在其他時間內,分子作直線運動。
基本介紹
- 中文名:氣體分子的平均自由程
- 氣體舉例:氫氣,氮氣,氧氣,二氧化碳等
由此得到的自由程與分子的速度有關,對各種速度求平均,就得到平均自由程。用平衡態的麥克斯韋分布求出的平均自由程有兩種。
① 麥克斯韋平均自由程。規定為氣體分子的平均速度與平均碰撞頻率之比。如此得到的平均自由程為
式中為分子的數密度,為分子的半徑。
② 泰特平均自由程。規定為氣體分子的速度與碰撞頻率之比的平均為=</>。如此算得的平均自由程為
1857年還未發現氣體分子的速度分布律,R.克勞修斯假定氣體分子的速率相同而方向不同,最先引入了自由程的概念。克勞修斯的自由程為。
通常所說的平均自由程是麥克斯韋平均自由程。利用理想氣體狀態方程=,可將平均自由程的公式換成溫度和壓強的函式
式中是玻耳茲曼常數。
標準狀態下,空氣分子的有效直徑為 3.5×10-10m,平均分子量為29,利用上述公式算出其平均自由程為=6.9×10m。可見,在標準狀態下,空氣分子的平均自由程約為其有效直徑的200倍。
氣體分子的平均自由程在氣體輸運的初級理論和真空技術、氣體放電等領域中,平均自由程都是常用的重要物理量。
 氣體分子的平均自由程
氣體分子的平均自由程 氣體分子的平均自由程
氣體分子的平均自由程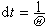 氣體分子的平均自由程
氣體分子的平均自由程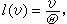 氣體分子的平均自由程
氣體分子的平均自由程 氣體分子的平均自由程
氣體分子的平均自由程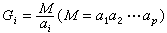 氣體分子的平均自由程
氣體分子的平均自由程 氣體分子的平均自由程
氣體分子的平均自由程 氣體分子的平均自由程
氣體分子的平均自由程 氣體分子的平均自由程
氣體分子的平均自由程 氣體分子的平均自由程
氣體分子的平均自由程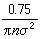 氣體分子的平均自由程
氣體分子的平均自由程 氣體分子的平均自由程
氣體分子的平均自由程 氣體分子的平均自由程
氣體分子的平均自由程