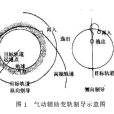
氣動輔助變軌是把純衝量變軌與氣動力變軌結合起來,在整個變軌飛行中插入大氣飛行段。在該段飛行中藉助氣動力完成部分變軌(改變軌道平面或高度),最終以最小耗能等技術指標完成全部變軌要求。
氣動輔助變軌可分為3個階段:共面離軌段、氣動輔助異面變軌段和共面升軌段。增量 Hohmann變軌公式可求。
基本介紹
- 中文名:氣動輔助變軌
- 外文名:aeroassisted orbital transfer
- 結合:純衝量變軌與氣動力變軌
研究的背景和意義,氣動力輔助變軌發展,氣動力輔助變軌,最優大氣輔助變軌研究的進展,稀薄氣體動力學發展現狀,有限推力變軌及其研究進展,軌道最佳化理論與最優控制的研究進展,氣動輔助變軌階段,氣動輔助轉移的方程,氣動力輔助變軌的套用,氣動力輔助軌道變換,星際探測,地球軌道轉移,
研究的背景和意義
未來的載人空間站系統是以空間站為核心,由同軌平台、極軌平台、自由飛行衛星及空間交通工具——軌道機動飛行器組成。軌道機動或轉移太空飛行器往 返於空間站與平台、衛星等飛行器之間,他們的變軌可用衝量或連續推力方 式,但是耗能比較大,而氣動力輔助軌道轉移可成為節省燃料的變軌方案。氣 動力輔助軌道轉移概念的提出始於六十年代,1961年H.London在美國宇航學 會上正式提交了一份論文,論證了氣動力輔助軌道轉移的意義與可行性。自此 揭開了氣動力輔助軌道轉移研究的序幕,四十多年來,世界各太空飛行器氣動力輔助變軌方法研究國的許多專家學者都參與了這一具有重大發展前景的課題的研究,尤其是自九十年代以後,關 於氣動力輔助軌道轉移的研究掀起了一個熱潮,從各個方面對氣動力輔助軌道 轉移問題進行了研究。
AOT(Aeroassisted Orbit Transfer)的概念最早由London提出的,並由其論 證了實現的可行性。所謂氣動力輔助軌道轉移,是把純衝量變軌與氣動力變軌結合起來,在整個變軌飛行中插入大氣飛行段。在該段飛行中藉助氣動力 完成部分變軌(改變軌道平面或高度),最終以最小耗能等技術指標完成全部變 軌要求。
氣動力輔助變軌與衝量變軌或者連續推力變軌比較,主要差別是:在完成 高能量到低能量軌道轉移時,前者能量消耗主要靠氣動力,後者主要靠燃料的 噴射;在完成軌道平面變換時,前者以氣動力為輔助手段完成部分軌道傾角變 化,後者主要靠燃料的反作用改變傾角;在設計轉移軌道時,前者需要有意插 入一段大氣層內軌道轉移,後者則無此要求。氣動力輔助變軌主要適用於低地 軌道和同步地球軌道或者其他深空高軌道之間的往返聯繫以及大軌道平面傾角 變化的異面軌道變軌。
AOT變軌方式由於有效的利用了太空飛行器環繞星球上的大氣這種自然資源,藉助氣動力減少了燃料消耗,從而使飛行器獲得了較大的有效載荷比。由 於這種變軌方式可以大大節省變軌所需的燃料,因此普遍認為AOT是未來空 間運輸的很重要的手段之一。我國將要發展先進的空間運輸系統,利用以上技 術會帶來巨大的經濟效益。因此這也就是研究氣動力輔助軌道轉移這個課題的原因。
氣動力輔助變軌發展
氣動力輔助變軌
1961年Howard London在美國宇航學會第二十九屆年會上正式提交了一 份論文,論證了套用AOT的意義和可行性。四十多年來,美、歐等國家的許 多專家、學者都在從事著方面的研究,在我國這項技術還處於起步階段,在近 些年來,哈爾濱工業大學、北京航空航天大學和西北工業大學等單位的部分專家學者已開始重視這項技術研究,並取得了一定的研究成果。
在對氣動力輔助軌道轉移的研究主要集中在兩個方面,第一階段主要針對氣動力輔助軌道轉移的最優軌跡的研究,第二階段是氣動力復轉軌道轉移的最 優控制律的研究。由於在AOT變軌過程中插入了大氣段飛行,故必須制定適 當的控制律控制,使OTV在大氣內完成相應的變軌要求,並最終能逸出大氣 到達目標軌道。
氣動力輔助變軌的套用主要有三個方面:
氣動力輔助軌道變換軌道平面變換是氣動力輔助軌道研究的最初研究目的,也是最早提出的, 典型的最優脫離軌道變軌如下:
首先,由特徵點a加一反向衝量ΔV1,使太空飛行器脫離HEO(High Earth Orbit) 進入轉移軌道,轉移軌道內切HEO於特點a,在大氣邊界特點b進入大氣 層,利用升力控制衛星在大氣層內的飛行,使之在c點衝出大氣層,同時在c 點施加第二個速度衝量ΔV2(如果速度足夠,c點可以不加衝量),使太空飛行器運行 至d點並於LEO(Low Earth Orbit)內切,同時加速度衝量ΔV,完成過渡全過 程,如圖1-1。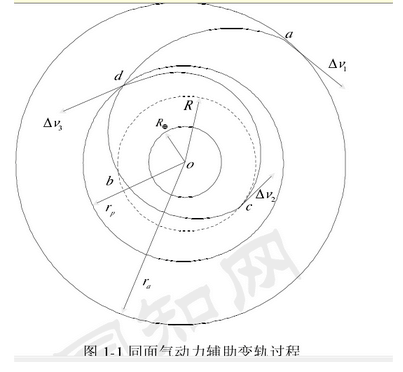

家學者已開始重視這項技術研究,並取得了一定的研究成果。
在對氣動力輔助軌道轉移的研究主要集中在兩個方面,第一階段主要針對
氣動力輔助軌道轉移的最優軌跡的研究,第二階段是氣動力復轉軌道轉移的最優控制律的研究。由於在AOT變軌過程中插入了大氣段飛行,故必須制定適 當的控制律控制,使OTV在大氣內完成相應的變軌要求,並最終能逸出大氣 到達目標軌道。
最優大氣輔助變軌研究的進展
一個太空飛行器在某個星球的大氣中飛行,將受到兩種自然力:氣動力和引力 的作用,氣動力是因飛行體與大氣的相對運動而誘發產生的,包括了星球的旋 轉和其他因素引起的大氣擾動。氣動力還是飛行體的氣動外形、飛行速度和高 度的函式,因而與逆平方率的引力不同。這種自然力的作用被人類認識研究並 加以利用,對人類文明和科學的演進產生了巨大影響。19世紀初數學、力學和 技術科學的蓬勃發展,促進了宇航科學的發展,人們對氣動力的作用有了系統 的理論認識,把它作為一個輔助利用來最佳化飛行體的軌道和最佳控制其飛行, 可獲得驚人的能量節省。
氣動力輔助變軌始於London所寫的有關衛星變軌的論文,自此以後,人 們對這個問題的研究取得了很大進展。Vinh在20世紀70年代就開始研究大氣 層中太空飛行器的運動特性和最佳化軌道理論。Walberg於1985年對氣動力輔助變軌 作了系統全面的總結與評述142篇文獻,Mease就氣動力輔助變軌的最佳化問 題作了評述,Miele近期就氣動力輔助變軌的最佳化與制導新進展作了較系統的 介紹,主要反映他和他的合作者的研究工作,綜述了99篇文獻。AOTV的 最優大氣輔助變軌,在大氣飛行段包括再入、大氣飛行及逸出大氣層等幾個階 段,過程比較複雜,而且在宇航工程套用中在產生經濟效益方面發揮出越來越 大的作用,故引起國內外許多科學家的廣泛重視,並開展了大量的研究工作。 Miele提出了大氣輔助變軌研究中的9種主要性能指標
1、動力變軌的燃料消耗量最小;
2、大氣飛行段的總加熱量最小;
3、大氣飛行段的飛行時間最小;
4、大氣飛行段的飛行時間最大;
5、大氣飛行段彈道傾角平方的積分最小;
6、進入與逸出大氣層的彈道傾角的平方和最小;
7、大氣飛行段的峰值熱流最小;
8、大氣飛行段的峰值動壓最小;
9、大氣飛行段的最低飛行高度最大。
前6類性能指標為化為終端型性能指標,後3種性能指標為Chebyshev型 性能指標。Miele和他的同事利用序列梯度恢復法對同面軌道、異面軌道的大 氣輔助過程進行了大量的計算。結果表明,對於平面大氣輔助變軌,性能指 標1和5的最優結果是類似的,對於異面變軌,利用性能指標5得到的結果雖然動力變軌的速度增量與性能指標1相比略有增加,但峰值動壓和峰值熱流大 幅度下降,因此,它提供的結果更為優越。
Vinh和Hull及其他作者,國內哈工大的楊滌、吳瑤華,西工大的陳 士櫓、呂學富等對大氣輔助平面變軌、異面變軌進行了研究,得到了大量 的結果。
Vinh和Lu P.推導了採用極大值原理處理Chebyshev問題的方法,將問題 化為沿軌道狀態變數受約束的問題來研究氣動滑行。Vinh和Mease研究了大 氣巡航的最優特性,指出這種輔助變軌方式對於大幅度改變近地軌道的傾角是 優越的。Vinh和Ma D.M.對多次通過大氣層的變軌過程進行了分析,因為一 次通過大氣層時,太空飛行器要承受很大的氣動加熱,而多次通過大氣層是一個較 好的解決辦法,但是,對於載人飛行,考慮到范阿倫輻射帶的影響,多次通過 大氣層時不適合的。
沿飛行軌跡最大加熱熱流,最大過載受到限制,這是基於結構質量和宇航 員的生理條件約束問題,Hiele.Chern和Vinh.Lee和Hull對這一問題進行了研 究,國內這方面研究比較少。
在未來的空間交會對接和反衛星武器系統中,氣動力輔助攔截和交會將會 起到非常重要的作用。它和一般的變軌不同之處主要在於終端條件,其最佳化目 標也不僅僅局限於燃料消耗最少,有時需要其攔截時間最小或軌道的傾角改變 量最大,以及脫靶量最小等,作為一般軍事目的的攔截和空間交會國內外研究 較多,但是這些研究都不是基於氣動力輔助變軌技術。Horie和Conway研究 推力為零情況下的氣動力輔助攔截問題,並就時間最小和耗能最小給出數值算 例。但是從軍事目的出發,最佳化目標函式往往是複合的,如時間最小和脫靶 最小,以及能耗最小和時間最小。另外推力協同氣動力輔助變軌,對增加攔截 和交會AOTV的機動性能和縮短飛行時間將具有現實工程套用意義。
推力協同在氣動力輔助變軌中的作用,儘管在20世紀60年代就有人研究 過,但是近年來又引起許多科學家的關注,並得到了許多新結論。Ross和 他的合作者以及Park,Caoalino等對氣動力輔助機動,協同機動,氣動力砰 擊,氣動力巡航機動等的研究,極大地推動了氣動力輔助變軌與控制的進展。 氣動力輔助變軌技術,已在星際航行得到了廣泛套用。值得進一步討論的是星際航行中利用星球的大氣層,實現輔助引力轉彎問題。氣動力輔助引力轉 彎時20年前美國捧起推進實驗室提出的一種氣動力輔助變軌概念,用於星際 航行變軌。當帶有升力體的飛行器飛過某星球的大氣層時,其升力矢量相對 星球體中心時,將比純引力轉彎獲得更大的速度增量,因而可降低發射能量和 縮短飛行時間。隨著星際探測任務被提到日程,對氣動力輔助引力轉彎的研究 越來越深入。
基於氣動力輔助變軌的變氣動外形飛行器的討論是作者今年的研究課題之 一。早在20世紀80年代Andrews,Grenich等人實驗性地研究充氣囊變 阻軌道器作為氣動制動的AOTV套用於空間運輸系統。這個新概念,近期被俄羅斯宇航界套用到再入飛行器和彈頭回收。太空飛行器的氣動外形對在大氣層 內飛行中的熱流、過載和機動性,以及最優成本都有決定性的作用。但是要滿 足全面的性能要求,很難找到一個理想的氣動外形,特別是一個固定的氣動外 形飛行器,因而,出現各種類型的帶有氣動制動器或捕獲裝置,或可變氣囊, 或可展的阻力裙,在給定的飛行階段,來改變飛行器的升阻比L/D和彈道系 數,以適應不同飛行任務要求。
稀薄氣體動力學發展現狀
研究超低軌道太空飛行器,就必須研究高層大氣產生的氣動力與氣動力矩對衛 星姿態和軌道的影響,由於超低軌道衛星飛行高度的環境中,大氣密度極低, 平均分子自由程與衛星特徵長度相比十分接近,因此氣動力方面的研究主要是 稀薄氣體動力學的研究。
國外在這方面早有理論上的研究,19世紀麥克斯韋利用平均自由程的概念 求得了氣體輸運係數,玻爾茲曼建立了分子運動速度分布函式的積分-微分方 程,即玻爾茲曼方程。1946年,錢學森最先利用努森數Kn,根據氣體的稀薄 程度將稀薄氣體流動分為四大領域:連續流領域、滑流領域、過渡領域、自由 分子流領域,並且提出了許多稀薄氣體動力學發展的關鍵性問題。至今,對於 解決稀薄氣體動力學問題的基本方法為解玻爾茲曼方程,具體實現有兩大類: 分析方法和數值方法。分析方法主要有矩方程或輸運方程方法、模型方程方 法、運動論邊值問題的變分方法等;而數值方法主要就是蒙特卡洛方法,又 被分為直接模擬蒙特卡洛方法(DSMC)、試驗單元蒙特卡洛方法(TPMC)等,這 類方法不解玻爾茲曼方程,而在計算機上用統計取樣模擬氣體分子的運動和碰 撞過程,其中澳大利亞的Bird提出的直接模擬蒙特卡洛方法在太空梭上得 到了實際的驗證;此外還有對碰撞積分進行數字積分,直接解玻爾茲曼方程 的方法,如間斷縱坐標方法等。
國內在這方面起步較晚,但是成果也有很多,主要有中科院的沈青在研究 改進直接模擬蒙特卡洛方法的計算機算法,提出了表面元算法來提高直接模擬 蒙塔特卡羅算法的效率,並且作為863計畫的一個項目研製了通用軟體;此 外,國防科技大學的吳其芬也在這方面編寫了一本稀薄氣體動力學專著[28]。 早期,太空飛行器氣動力與氣動力矩的計算基本採用近似的方法,假定某一氣動阻力係數,帶入解析式計算出氣動力後,假設質心與壓心之間的矢徑是包括 全部附屬檔案在內的太空飛行器最大尺寸的三分之一,進而通過力乘力臂的方式得到 衛星受到的氣動力矩,但是這僅僅是保守的估計值。當前,出現了計算機後, 對氣動力與氣動力矩的計算就有了很大的發展。對於氣動力計算的軟體編制方 面,國外已經有比較完善的理論計算公式和計算方法來進行建模和程式編制, 其中就包括經驗公式和直接模擬蒙特卡洛方法。早期的衛星設計者們使用的主 要是經驗公式。當前,國外已經發展了許多計算軟體:直接模擬蒙特卡洛方法 的創立者Bird開發了DS2V/DS3V程式,能夠對二維或三維任意外形物體的氣 動力與氣動力矩進行直接模擬蒙特卡洛方法的計算,程式說明也比較詳細,主 要問題就是軟體中導入三維模型的前期處理繁瑣並需要其他特殊的軟體,計算 氣動力與氣動力矩的時間比較長,占用大量CPU和記憶體,並沒有提示說明計哈爾濱工業大學工學碩士學位論文算結果已經收斂穩定;英國Cranfield大學的空間研究中心研發了環數據分析工具(Spacecraft Engineering,Design,and Analysis Tools:SEDAT)軟體,利用的是自由分子流的公式並結合氣體與物體表面反應的模型、光線追蹤方法和試驗單元蒙特卡洛方法進行的編程,而且已經為歐空局的空間碎片收集衛星計畫進行了計算,但是龐大而複雜的數據對計算過程產生了巨大的影響。另外,俄羅斯也根據直接模擬蒙特卡洛方法研製了計算氣動力的軟體 SMILE(Statistical Modeling In Low-Density Environment),Ivanov等人計算了進 步號飛船的氣動力。
在國內,這方面的氣動力計算主要套用於載人太空飛行器返回的精確制導,預 估返回艙進入大氣層飛行期間的各向載荷分布,評估氣動穩定性,確定飛行軌道。載人飛船返回經歷的自由分子流和過度流區,主要採用蒙特卡洛方法和近 似計算方法來得到氣動力量值。
有限推力變軌及其研究進展
自從R.H.Goddard對在兩點間的太空飛行器最優轉移軌道問題提出在能量消耗 最少情況下的最優近似解法以來,這一問題引起了學術界的廣泛關注。1959 年,Hohman解決了在共面圓軌道間轉移的最小特徵速度這一基本問題。此 後,Marec從理論上做出了精確的證明,Marchal把Hohmann理論套用於橢圓軌道間的轉移,Smith研究了橢圓和圓軌道之間的轉移,McCue則研究了 非共面軌道之間的轉移,Eckela和vinh研究了固定時間和固定燃料下的 Hohmann軌道轉移問題。
Hoelker和Silber第一次提出三次變軌問題並驗證了這種變軌要優於 Hohmann轉移。Roth藉此研究了非共面橢圓軌道間轉移。之後,Prussing、 Glickman和Bercaw進行了多次衝量下的最優軌道轉移問題的研究。Redding 和Matogawa繼續將這一思想加以推廣,得出了軌道以有限推力進行多次變軌 能夠達到最優的結果。
還有一些學者進行脈衝式變軌研究是通過轉移次數作為變數而不是固定的 值,從事這方面的工作者主要有Handelsman,Jezewski和Rosendaal,Gross和 Prussing,Eckel、Prussing和Chiu。該方法的出發點是Lawden開創的矢量 力學。Antoi Fernando BertaChinide Almeida Prod通過數值方法進行有限推力下哈爾濱工業大學工學碩士學位論文的軌道轉移問題研究,該方法先用於推力方向固定的情況下,然後對推力方向 進行多次取初值來計算能量損失,通過比較不同的結果找到最優方案。可見, 該方法的計算量是較大的,而且假定變軌過程中推力方向不變是有局限性的。 但是在實際的工作過程中,沒有必要假定推力方向不變,發動機推力方向是時 時變化的,這樣對節省能量也是有好處的。
軌道最佳化理論與最優控制的研究進展
在有限推力變軌、大氣輔助變軌的最最佳化研究中,我們所要尋找的是一條 最優飛行軌跡,這是過程最佳化或最優控制問題,從工程套用角度稱為軌跡優 化,這類問題很早就得到了科技界的重視。從20世紀30年代開始,Caratheodory在古典變分法基礎上開始研究最最佳化方法,但是直到計算機的出 現,最最佳化方法才真正用於工程實踐中。例如20世紀50年代,錢學森用古 典變分法研究了探空火箭在大氣中的垂直上升的最大飛行高度問題,獲得了滿 意的結果,並在以後的探空火箭設計中得到了套用,這項工作對以後的軌跡優 化研究產生了重要的影響。
古典變分法所能解決的問題是有限的,它無法處理某些變數受到約束或發 生突變的情況,即使對於探空火箭垂直上升這樣一個簡單問題,也必須作大量 的假設,而所得結果還包含起飛衝量這樣一個實際設計中難以實現的過程。20 世紀50年代,俄羅斯學者Pontryagin等人在古典變分法的基礎上,將變數 區分為狀態變數和控制變數,討論了有界控制下純狀態約束的最佳化問題,給出 了龐特里壓金極大值原理的共同點就是通過最優性能分析,控制函式能夠表示 成狀態變數和附加的伴隨變數函式,然後化為兩點邊值問題求解,由於不是對 性能指標函式直接尋優,因此稱為間接法。常用數值方法求解,一種最廣泛的 方法是打靶法和多次打靶法。龐特里壓金的合作者之一格姆克列里茲在他的研 究中,對最優控制理論中的變分法作了完整的、嚴格的證明。Hartl等人就具有狀態約束的最優控制問題的極大值原理和其套用作了全面的介紹。
國內有許多學者在這個領域作了很深研究。傑出科學家錢學森在二次世界 大戰結束前後對彈道火箭及其控制的研究中,特別是解決最佳化方法與反饋控制 技術和理論問題,發展成一門新的學科——工程控制論,並在1945年出版了 《Engineering Cybernetics》,為世人所矚目,是該領域最早的開拓者 。哈爾濱工業大學工學碩士學位論文值得指出,控制論學者Berkovitz於1961年就提出變分方法,1974年對優 化控制過程給出嚴格的數學理論。Bell和Jacobson在1975年就系統的研究奇 異最佳化控制理論。隨著推力協同引入氣動力輔助變軌,奇異最佳化控制問題今年 來受到學術界極大的關注,並取得突破性進展,集中表現在對極值弧,特別是 奇異弧,開關結構的特性,連線條件和相關的控制律研究,這些研究有力的推 動了飛行器的最佳化設計,並對過去長期研究結論提出質疑。
直接解法較間接法大約早了一個世紀,可追溯到1874年Cauchy的梯度法。20世紀50年代,貝爾曼,Bryson,Denham,Mikamn等人研究了求解最 優過程問題的數值方法,如貝爾曼動態規劃法、一階梯度法、二階梯度法等, 尤其值得注意的是貝爾曼動態規劃法,它的解是全局最優解。Miele等人從60 年代開始研究序列梯度恢復法,近十年來用該方法對最優大氣輔助變軌過程進 行了研究,證明是一種較好的方法。Betts,Enright等人討論了稀疏非線性規劃法、非線性規劃法以及直接有限元轉移法等,Hargraves和Herman等人討 論了直接配點非線性規劃法,以及最近Fahroo和Ross的Legendre偽譜線法是十分有效簡便方法。這些方法將方程沿飛行軌跡離散化,微分方程作為離散變數之間的約束,直接採用參數最佳化的方法進行求解。這些方法的共同特點是對指標函式直接尋優,因此成為直接法。直接法的最近進展是套用微分幾何的微分包含來表示一個動力學系統的狀態變數導數所構成的一個集,並將狀態速率約束在一個可行的空間。由此最佳化解僅僅是狀態變數在節點上的離散,而不必考慮控制變數,故既是低維的,又適用奇異控制問題的求解,且增加了魯棒性。
氣動輔助變軌階段
氣動輔助變軌方法
並假設切向速度增量 等於法向速度增量除以最大升阻比(取 1.8),且為負值。 高度的圓軌道所需速度氣動輔助變軌可分為3個階段:共面離軌段、氣動輔助異面變軌段和共面升軌段。增量 Hohmann變軌公式可求。
HEO-LEO 共面變軌,初始 HEO 軌道為赤道圓軌道,軌道半徑為 r1;目標 LEO 軌道亦為赤道圓軌道, 軌道半徑為 r2。
a)共面離軌段:首先施加一個離軌速度增量 橢圓轉移軌道,橢圓轉移軌道的近地點在大氣層內,兩者處於同一軌道面內。
b)氣動輔助異面變軌段:進入大氣層後,進行氣 動輔助異面變軌機動,獲得法向速度增量,完成軌道 平面的改變。
a)共面升軌段:氣動輔助異面變軌完成後,飛行 器到達大氣層的邊緣並施加一次脈衝軌道機動加速軌 因此,得到 LEO-LEO 異面變軌節省燃料條件為: 在對應的圓軌道高度上,軌道傾角 改變大於臨界變軌角度時,氣動輔助變軌才節省燃料。 道機動 橢圓軌道。當到達橢圓軌道的遠地點時,再施加一次速度增量 如果想通過氣動輔助變軌節省燃料,其任務剖面必須滿足一定的條件:
1)對於 HEO-LEO 共面變軌,對應不同的目標圓 軌道高度,當初始圓軌道高度大於表 中對應的臨界初始圓軌道高度時,氣動輔助變軌才節省燃料。
2)對於 LEO-LEO 異面變軌,對應不同的圓軌道 高度,當軌道傾角 改變大於表 中對應的臨界變軌角度時,氣動輔助變軌才節省燃料。
氣動輔助轉移的方程
假設行星的大氣是不旋轉的,並且大氣的密度隨高度以指數變化。探測器在大氣中的運動方程如下:
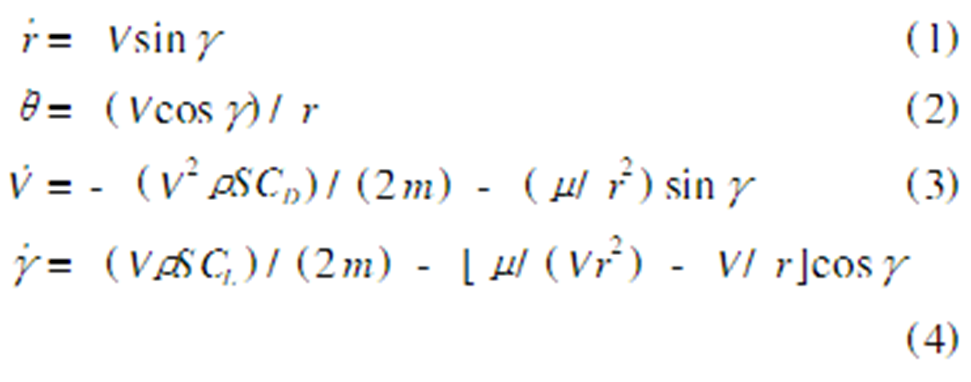
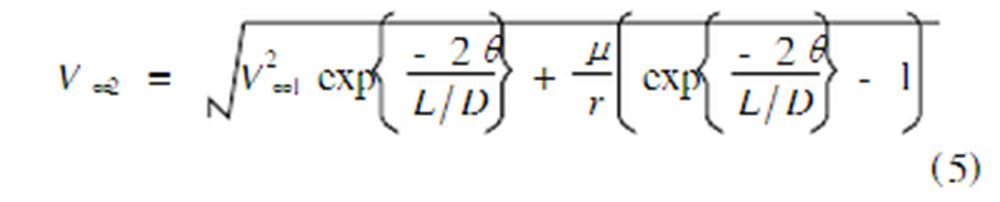
這裡μ和r分別是借力天體的引力常數和探測器距離借力天體中心的半徑。探測器在大氣中飛過的轉角θ可由下式得到:
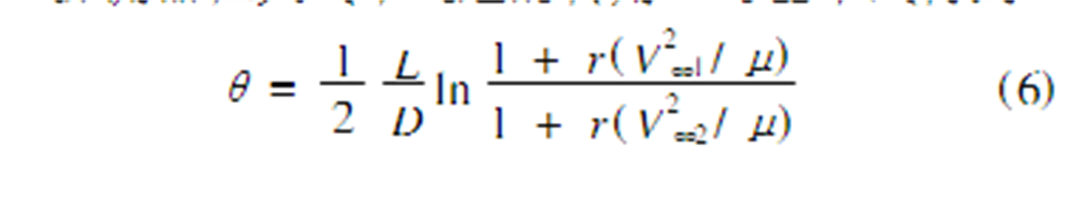
AGA轉移總的轉角<為飛入大氣前後引力產生的轉角與大氣中飛過的轉角之和,即:
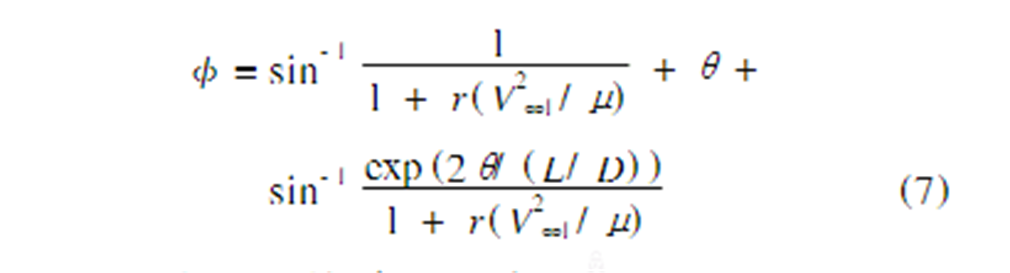
由以上這些關係可以看出:V∞1、L/D和θ是三個影響AGA軌道設計的重要參數,而AGA轉移所產生的速度變化量ΔV、大氣轉角θ的邊界以及AGA轉移軌道的拼接條件是AGA軌道設計中值得關注的幾個問題。
氣動力輔助變軌的套用
氣動力輔助軌道變換
軌道平面變換是氣動力輔助軌道研究的最初研究目的,也是最早提出的, 典型的最優脫離軌道變軌如下:
首先,由特徵點a加一反向衝量Δv1,使太空飛行器脫離HEO(High Earth Orbit) 進入轉移軌道,轉移軌道內切HEO於特點a,在大氣邊界特點b進入大氣 層,利用升力控制衛星在大氣層內的飛行,使之在c點衝出大氣層,同時在c 點施加第二個速度衝量Δv2(如果速度足夠,c點可以不加衝量),使太空飛行器運行 至d點並於LEO(Low Earth Orbit)內切,同時加速度衝量Δv3,完成過渡全過程
星際探測
星際飛行中的氣動力輔助套用,又可以分為不同的兩類:大氣捕獲和大氣 制動。二者都是利用氣動力使飛行器獲得必要的速度衰減,太空飛行器從雙曲線接 近軌道進入繞行星的目標軌道,顯然,只能套用於有大氣環繞的行星,如:火 星,當然也可以套用於行星際飛行器返回地球的飛行。在大氣捕獲過程中,太空飛行器有很大的升力速度進入行星大氣層,用滾動調節獲得常值阻力,從而產生速度衰減,退出大氣後用一個小火箭圓化,大氣捕 獲對未來的火星探測是必須要套用的。
大氣制動時通過多次穿越大氣。而使太空飛行器的速度利用大氣阻力降下來達到制動的目的,其過程大致是:首先制動火箭點火,使太空飛行器從接近軌道進入 高扁率的橢圓軌道,通過多次穿越外層大氣而使軌道逐漸圓化,為了使太空飛行器 既要獲得足夠的阻力用以衰減速度,又要避免產生過大的空氣動力加熱,每次穿越大氣後在遠地點都要修正火箭點火,保證近心點高度。
地球軌道轉移
地球軌道轉移的背景是現代和未來的航天中,需要把太空飛行器或其他載荷從 地球低軌道的運行系統如太空梭,空間站等,運送到地球高軌道運行的飛行 器。由於這些載荷可能包括太空人等有生命的載荷,所以要求軌道轉移太空飛行器 應具有可重複使用的能力,同時利用氣動力輔助軌道轉移更能提高軌道轉移飛 行器的有效載荷比,這種軌道既有軌道高度的變化,也有軌道傾角的變化,它是三類氣動輔助套用的最高形式。
二十一世紀,空間站和高級空間運輸系統將成為重要的發展方向,而我國也將獨立發展自己空間站和高級空間運輸系統,由於氣動輔助軌道轉移具有節 省燃料的強大優勢,同時這種變軌方式又適用於軌道轉移太空飛行器,因此氣動輔 助軌道轉移的研究是十分必要的,而且具有很強的科學與工程意義。