簡介
飛行器的氣動模型基於自身動力學方程與運動學方程,描述了其姿態、速度、位置等運動參數與飛行器氣動參數以及飛行控制量之間的關係。在飛行器氣動結構參數與飛行控制量已知的條件下,結合動力學原理,氣動模型可以獨立自主地提供飛行器的姿態、角速度、速度、加速度等運動信息。由於這些運動信息與飛行器導航所需參數有著直接的聯繫,將其與已有導航系統的輸出信息進行融合,能夠在一定程度上提高飛行器的自主導航精度與可靠性。
非定常空氣動力建模
隨著研究非定常空氣動力遲滯特性的大振幅動態風洞試驗的開展,對非定常空氣動力建模的研究也逐漸發展起來。對於非定常空氣動力建模,在二十世紀初已經在國外出現,但是直到大約二十世紀八十年代,非定常空氣動力建模才廣泛進行研究,陸續地發展了多種非定常氣動力建模方法。Tobak首先將階躍函式的概念套用到非線性空氣動力方面,通過階躍函式建模來研究二維翼型、機翼和飛機模型的非定常空氣動力回響。該方法利用Fourier變換來確定系統非定常回響的階數,進而確定空氣動力模型。但是
Fourier僅僅適用於穩態信號分析,而對於非線性非定常氣動力基本是非穩態信號,因此通過階躍函式建立非定常空氣動力模型不太適用。Lin等人採用了非線性代數模型進行非定常氣動力建模研究,這種方法實際上是利用泰勒級數將非定常氣動力表示為飛行狀態變數的高階多項式的形式,但它不完全是泰勒級數展開,可看作是修正的泰勒級數展開。非線性代數模型表達式的寫法在某種程度上是任意的,它可分為二階非線性代數模型、三階非線性代數模型和四階非線性代數模型等。該方法的不足之處在於用於模型的建模變數不可過多,如果超過3個,由於非線性代數模型的表達式的形式不好確定,模型參數很難辨識,所以該方法很難實現。
狀態空間法的模型表達形式相對簡單,對於建模方面的研究比較方便。但是一方面該方法受模型表面流動分離點位置的影響較大,由於飛機構型的複雜性,流動分離點不易確定,因此該模型存在較大誤差;另一方面該模型中非線性項的物理意義不十分明確,將其用作建模研究還有待進一步改進。汪清等人將狀態空間法改造為一階微分方程的形式,即採用慣性系統理論來描述飛機的大振幅運動過程。他根據流動分離的形式將非定常氣動力分成兩部分,但是這種拆分氣動力的方法很難實現,並且拆分的氣動力也很難精確,因此該模型使用不便並且精度不高。在九十年代後期,氣動力建模中出現了基於神經網路和模糊邏輯原理的建模方法。對於採用模糊邏輯原理進行的氣動力建模,通過研究隸屬函式的選取,來調整建模的精度。這種建模方法的好處在於不限制建模變數的個數,增加建模變數的個數,僅僅會導致建模時間的增加,並不會對模型的套用造成影響。而研究耦合運動非定常空氣動力特性可以發現,具有遲滯特性的非定常空氣動力會受到很多運動狀態參數的影響,該非定常氣動力是多變數的函式。因此,模糊邏輯原理是很適用於進行耦合運動的非定常空氣動力建模研究。但是,目前國內外的研究水平,僅停留在單自由度建模方法上,還沒有向兩自由度以及多自由度的氣動建模上拓展。對於基於神經網路原理的氣動建模與模糊邏輯建模情況大致一樣。
隨著戰鬥機機動性能的不斷提高,
風洞試驗水平的不斷增強,提供飛行過程中動態氣動力的相應空氣動力數學模型也在不斷發展。空氣動力分為定常氣動力和非定常氣動力兩大部分,由於大振幅運動風洞試驗的開展,非定常氣動力的研究成為目前氣動研究的重點。對於非定常空氣動力,至今國內外還廣泛採用基於小擾動線性疊加原理的非定常空氣動力模型。處理耦合運動時的非定常空氣動力通常採用單自由度運動結果相疊加,有基於單自由度大振幅運動風洞試驗的線性疊加模型,基於動導數試驗的動導數疊加模型,以及基於動導數試驗和旋轉天平試驗的混合模型。以上空氣動力模型在小攻角時經過長期考察是可用的,但是在大攻角時,飛機受到的空氣動力有很強的遲滯特性,線性疊加模型能否描述這一耦合遲滯、是否適用於大攻角還有待研究。
氣動模型輔助導航
氣動模型輔助導航方法具有自主性強、成本低、適用範圍廣等優點。飛行器氣動模型利用大氣數據信息進行運動參數的解算,這些信息測量的感測器大多基於機械力學和運動學特性,不會出現信號受外界遮擋等情況,極大程度上提高了導航系統的自主性。由於氣動模型僅需要利用飛行器飛行必備的感測器,不需要額外的硬體設備就可以解算出導航中所需的運動參數,大大降低了導航系統的製作成本。氣動模型輔助導航方法自主性強、成本低的特點有利於擴展導航系統的適用對象和套用範圍。例如對於炮彈等一次性武器,函需能保證打擊精度的低成本導航系統來完成作戰任務。與傳統導航方式相比,氣動模型輔助已有的導航系統可以進一步滿足無人機對高精度、高可靠性導航系統的需求。
氣動模型輔助導航方法的提出起始於20世紀90年代末,其目的為利用飛行器自身的動力學特性與運動信息輔助低精度慣性導航系統,以提高系統的導航性能。之後該方法得到了國外學者的關注,在氣動模型輔助導航的可行性、有效性以及濾波方案設計等方面進行了較為廣泛的討論。根據氣動模型輔助的導航系統對象不同,可將其分為三種技術方案:氣動模型輔助慣性導航系統,氣動模型輔助
衛星導航系統,以及氣動模型輔助慣性/衛星
組合導航系統。
國外研究人員針對氣動模型輔助慣性導航系統的可行性、濾波方案展開了深入地研究。1999年,以色列理工學院的學者M. Koifman首次提出了氣動模型輔助慣性導航的概念,並對其進行了原理上的研究驗證。研究中以固定翼飛行器為對象,建立了完整的氣動模型以及全信息數據融合方案中狀態方程、量測方程,其濾波器結構如圖1。仿真中根據規劃的飛行軌跡進行了驗證,結果表明低精度慣性導航系統在氣動模型的輔助下,其位置、速度、姿態角等導航參數的解算精度較原系統有顯著提高。相應的研究成果驗證了氣動模型輔助慣性導航系統的可行性。另外,研究中利用不同精度的氣動模型對輔助慣性導航系統進行輔助,並對組合導航效果進行了比較,表明氣動模型的精度提高是後期技術發展的關鍵。
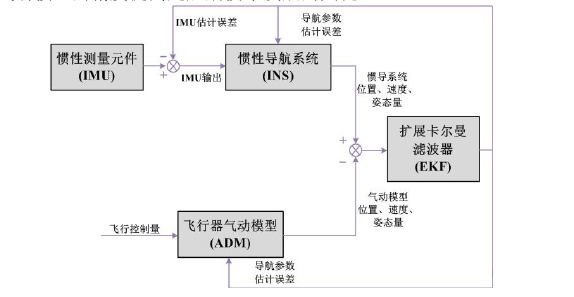
圖1 飛行器氣動模型 / 慣性導航系統的濾波結構
2005年,
代爾夫特理工大學的K.P.A. Lievens提出了一種氣動模型輔助單GPS完成測姿任務的方法,其採用Cessna飛行器,通過試驗對提出的方法進行了驗證。結果表明該方案能夠在降低套用成本和飛行器負載的情況下,獲得與機載測姿設備精度相當的姿態數據。2011年
英國坎特伯雷大學博士T.P. James研究了小型固定翼飛行器中輔助單個GPS進行測姿的兩種方案。仿真結果證明利用氣動模型輔助GPS的測姿方案在精度方面優於運動約束條件輔助GPS的測姿方案。
瑞士聯邦理工學院的Christoph Eck早在2001年提出一種套用於無人機的氣動模型/慣性導航/GPS新型導航方案,其目在於提高GPS失效時純慣性導航系統的精度。當能夠獲得GPS信號時,利用GPS/慣性導航系統數據不斷修正飛行器氣動模型,提高模型準確性;當無法獲得GPS信號時,則採用氣動模型/慣性導航的方案進行導航,系統流程如圖2。研究表明,在GPS短時失效時氣動模型/慣性導航/
GPS導航方案可以提高系統導航精度,但
GPS長時間失效仍會導致誤差的發散。
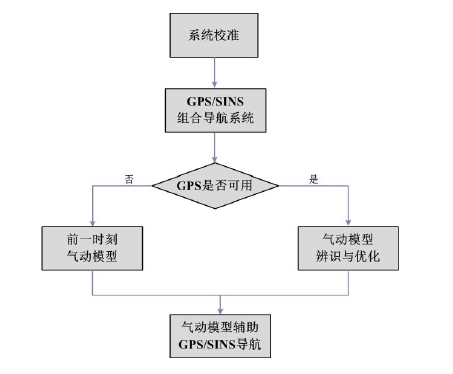
圖2 氣動模型輔助 GPS/SINS 導航系統流程圖



