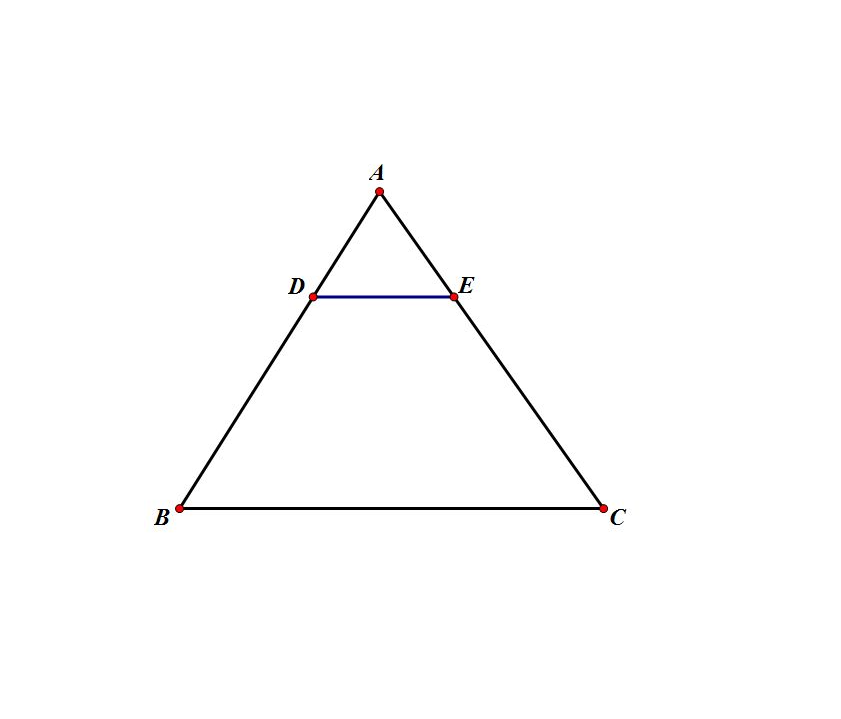
如果四條線段a,b,c,d滿足a/b=c/d,則四條線段a,b,c,d稱為比例線段。(有先後順序,不可顛倒)
比例的基本性質:如果a/b=c/d,那么ad=bc; 如果ad=bc,且abcd≠0,那么a/b=c/d; 如果a/b=c/d,那么(a±b)/b=(c±d)/d。abcd都不能為0。為0無意義。
基本介紹
- 中文名:比例線段
- 外文名:Proportional line segment
- 含義:兩條線段長度比叫做這兩條線段比
- 性質:4條線段成比例
- 套用:幾何計算
- 學科:數學
比例,基本概念,證明過程,比例性質,
比例
比例,技術製圖中的一般規定術語,是指圖中圖形與其實物相應要素的線性尺寸之比。表示兩個比相等的式子叫做比例,如3:4=9:12、7:9=21:27
在3:4=9:12中,其中3與12叫做比例的外項,4與9叫做比例的內項。比例的四個數均不能為0。
比例有四個項,分別是兩個內項和兩個外項;在7:9=21:27中,其中7與27叫做比例的外項,9與21叫做比例的內項。
比例有四個項,分別是兩個內項和兩個外項。
如果選用同一個長度單位量得兩條線段AB、CD的長度分別是m,n,那么這兩條線段的比就是它們長度的比,即AB:CD=m:n,其中,線段AB,CD分別叫做這個線段比的前項和後項,如果把m:n表示成比值k,那么AB:CD=k,或AB=k·CD。兩條線段的比實際上就是兩個數的比。
基本概念
1.兩條線段的長度比叫做這兩條線段的比。
2.在同一單位下,四條線段長度為a、b、c、d,其關係為a:b=c:d,那么,這四條線段叫做成比例線段,簡稱比例線段。
4.d為第四比例項。
若a:b=c:d(b.d≠0),則有
1) ad=bc
2) b:a=d:c (a.c≠0)
3) a:c=b:d ; c:a=d:b
4) (a+b):b=(c+d):d
5) a:(a+b)=c:(c+d) ( a+b≠0,c+d≠0)
6) (a-b):(a+b)=(c-d):(c+d) ( a+b≠0,c+d≠0)
7)若有a+b=c+d 則a=c,b=d
證明過程
如下
令 a:b=c:d=k,
∵a:b=c:d
∴a=bk;c=dk
1)∴ad=bk*d=kbd;bc=b*dk=kbd
∴ad=bc
2) 顯然b:a=d:c=1/k
3) a:c=bk:dk=b:d ;結合性質2有c:a=d:b
4) ∵a:b=c:d
∴(a/b)+1=(c/d)+1
∴(a+b)/b=(c+d)/d=1+k ;即 (a+b):b=(c+d):d
a+b≠0,c+d≠0時,結合性質2有b:(a+b)=d:(c+d)
且b/(a+b)=d/(c+d)=1/(k+1) ……①
5) ∵b/(a+b)=d/(c+d)
∴1- b/(a+b)=1- d/(c+d)=1-1/(k+1)
∴a/(a+b)=c/(c+d)=k/k+1 ……② 即a:(a+b)=c:(c+d)
a+b≠0,c+d≠0時,結合性質2有 (a+b):a=(c+d):c
6) ②-①,等式兩邊同時相減得 (a-b)/(a+b)=(c-d)/(c+d) =(k-1)/(k+1)
7)根據(4)可得a=c,b=d
比例性質
比例的基本性質:a/b=c/d ad=bc
比例的合比性質:a/b=c/d (a+b)/b=(c+d)/d
(注意:在分子上加分母)
比例的分比性質:a/b=c/d (a-b)/b=(c-d)/d
比例的等比性質:若 a/b=c/d=…=m/n(b+d+…+n≠0),
則 (a+c+…+m)/(b+d+…+n)=a/b=c/d…=m/n
比例的反比性質:a/b=c/d b\a=d\c
比例的更比性質:若 a/b=c/d 則 a/c=b/d
比例線段:若4條線段成比例,則4條線段稱為比例線段
[平行線分線段成比例]
2直線截3條平行線,則對應線段成比例
當l1 ,l2 ,l3互相平行時,AB:BC=DE:EF,AD:BE=BE:CF
[套用]
地圖的比例尺。