基本介紹
- 中文名：殘差網路
- 外文名：Residual Network, ResNet
- 類型：卷積神經網路
- 提出者：Kaiming He，Xiangyu Zhang，
- 自定義：Shaoqing Ren，Jian Sun
- 提出時間：2015年
背景,解決退化問題,相關工作,殘差表示,shortcut連線,深度殘差學習,殘差學習,通過shortcut同等映射,網路結構,實驗,深層探究,
背景
該網路出自論文《Deep Residual Learning for Image Recognition》
我們都知道增加網路的寬度和深度可以很好的提高網路的性能，深的網路一般都比淺的的網路效果好，比如說一個深的網路A和一個淺的網路B，那A的性能至少都能跟B一樣，為什麼呢？因為就算我們把B的網路參數全部遷移到A的前面幾層，而A後面的層只是做一個等價的映射，就達到了B網路的一樣的效果。一個比較好的例子就是VGG，該網路就是在AlexNet的基礎上通過增加網路深度大幅度提高了網路性能。
對於原來的網路，如果簡單地增加深度，會導致梯度彌散或梯度爆炸。對於該問題的解決方法是正則化初始化和中間的正則化層（Batch Normalization），這樣的話可以訓練幾十層的網路。
雖然通過上述方法能夠訓練了，但是又會出現另一個問題，就是退化問題，網路層數增加，但是在訓練集上的準確率卻飽和甚至下降了。這個不能解釋為overfitting，因為overfit應該表現為在訓練集上表現更好才對。退化問題說明了深度網路不能很簡單地被很好地最佳化。作者通過實驗：通過淺層網路等同映射構造深層模型，結果深層模型並沒有比淺層網路有等同或更低的錯誤率，推斷退化問題可能是因為深層的網路並不是那么好訓練，也就是求解器很難去利用多層網路擬契約等函式。
解決退化問題
深度殘差網路。如果深層網路的後面那些層是恆等映射，那么模型就退化為一個淺層網路。那當前要解決的就是學習恆等映射函式了。 但是直接讓一些層去擬合一個潛在的恆等映射函式
，比較困難，這可能就是深層網路難以訓練的原因。但是，如果把網路設計為
,如圖1。我們可以轉換為學習一個殘差函式
。 只要
，就構成了一個恆等映射
。 而且，擬合殘差肯定更加容易。
圖1 殘差函式
F是求和前網路映射，H是從輸入到求和後的網路映射。比如把5映射到5.1，那么引入殘差前是
，引入殘差後是
，
，
。這裡的F'和F都表示網路參數映射，引入殘差後的映射對輸出的變化更敏感。比如s輸出從5.1變到5.2，映射
的輸出增加了2%，而對於殘差結構輸出從5.1到5.2，映射F是從0.1到0.2，增加了100%。明顯後者輸出變化對權重的調整作用更大，所以效果更好。殘差的思想都是去掉相同的主體部分，從而突出微小的變化。
至於為何shortcut的輸入是X，而不是X/2或是其他形式。作者的另一篇文章中探討了這個問題，對以下6種結構（圖2）的殘差結構進行實驗比較，shortcut是X/2的就是第二種，結果發現還是第一種效果好。
圖2 6種結構
這種殘差學習結構可以通過前向神經網路+shortcut連線實現，如結構圖1所示。而且shortcut連線相當於簡單執行了同等映射，不會產生額外的參數，也不會增加計算複雜度。 而且，整個網路可以依舊通過端到端的反向傳播訓練。
ImageNet上的實驗證明了作者提出的加深的殘差網路能夠比簡單疊加層生產的深度網路更容易最佳化，而且，因為深度的增加，結果得到了明顯提升。另外在CIFAR-10數據集上相似的結果以及一系列大賽的第一名結果表明ResNet是一個通用的方法。
相關工作
殘差表示
VALD，Fisher Vector都是是對殘差向量編碼來表示圖像，在圖像分類，檢索表現出優於編碼原始向量的性能。
在low-level的視覺和計算機圖形學中，為了求解偏微分方程，廣泛使用的Multigrid方法將系統看成是不同尺度上的子問題。每個子問題負責一種更粗糙與更精細尺度的殘差解析度。Multigrid的一種替換方法是層次化的預處理，層次化的預處理依賴於兩種尺度的殘差向量表示。實驗表明，這些求解器要比對殘差不敏感的求解器收斂更快。
shortcut連線
shortcut連線被實驗和研究了很久。Highway networks也使用了帶有門函式的shortcut。但是這些門函式需要參數，而ResNet的shortcut不需要參數。而且當Highway networks的門函式的shortcut關閉時，相當於沒有了殘差函式，但是ResNet的shortcut一直保證學習殘差函式。而且，當Highway networks的層數急劇增加時，沒有表現出準確率的上升了。總之，ResNet可以看成是Highway networks的特例，但是從效果上來看，要比Highway networks好。
深度殘差學習
殘差學習
根據多層的神經網路理論上可以擬合任意函式，那么可以利用一些層來擬合函式。問題是直接擬合
還是殘差函式，擬合殘差函式
更簡單。雖然理論上兩者都能得到近似擬合，但是後者學習起來顯然更容易。
圖3 殘差學習
作者說，這種殘差形式是由退化問題激發的。根據前文，如果增加的層被構建為同等函式，那么理論上，更深的模型的訓練誤差不應當大於淺層模型，但是出現的退化問題表明，求解器很難去利用多層網路擬契約等函式。但是，殘差的表示形式使得多層網路近似起來要容易的多，如果同等函式可被最佳化近似，那么多層網路的權重就會簡單地逼近0來實現同等映射，即
。
實際情況中，同等映射函式可能不會那么好最佳化，但是對於殘差學習，求解器根據輸入的同等映射，也會更容易發現擾動，總之比直接學習一個同等映射函式要容易的多。根據實驗，可以發現學習到的殘差函式通常回響值比較小，同等映射（shortcut）提供了合理的前提條件。
通過shortcut同等映射
用來學習殘差的網路層數應當大於1，否則退化為線性。文章實驗了layers = 2或3，更多的層也是可行的。
用卷積層進行殘差學習：以上的公式表示為了簡化，都是基於全連線層的，實際上當然可以用於卷積層。加法隨之變為對應channel間的兩個feature map逐元素相加。
網路結構
作者由VGG19設計出了plain 網路和殘差網路，如圖3中部和右側網路。然後利用這兩種網路進行實驗對比。
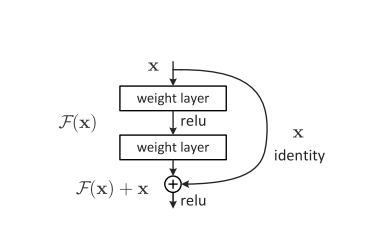
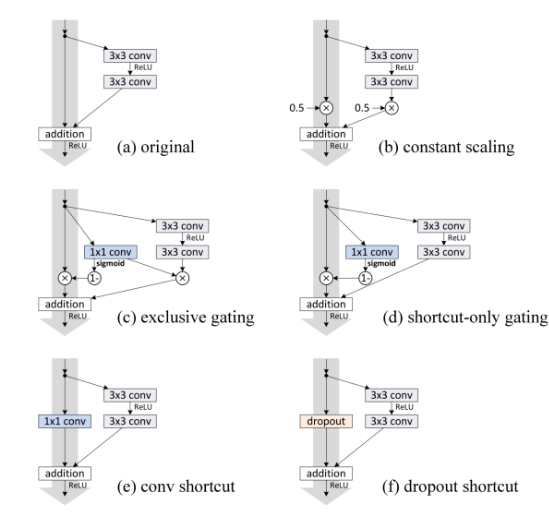
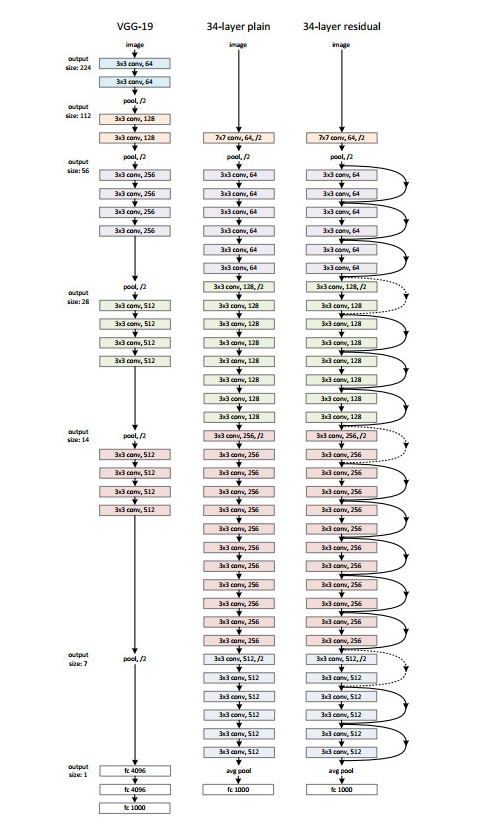
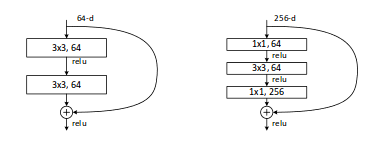
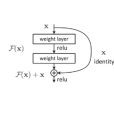
設計網路的規則：1.對於輸出feature map大小相同的層，有相同數量的filters，即channel數相同；2. 當feature map大小減半時（池化），filters數量翻倍。
對於殘差網路，維度匹配的shortcut連線為實線，反之為虛線。維度不匹配時，同等映射有兩種可選方案：
- 直接通過zero padding 來增加維度（channel）。
- 乘以W矩陣投影到新的空間。實現是用1x1卷積實現的，直接改變1x1卷積的filters數目。這種會增加參數。
編程實現
這裡以ResNet-50為例提供一個殘差網路在Tensorflow和Keras下的編程實現：
import tensorflow as tf
from tensorflow import keras
# 按 He et al. (2016) 定義兩類殘差塊。
def identity_block(X, f, channels):
'''
卷積塊--(等值函式)--卷積塊
'''
F1, F2, F3 = channels
X_shortcut = X
# 主通路
# 塊1
X = keras.layers.Conv2D(filters=F1, kernel_size=(1, 1), strides=(1,1), padding ='valid')(X)
X = keras.layers.BatchNormalization(axis=3)(X)
X = keras.layers.Activation('relu')(X)
# 塊 2
X = keras.layers.Conv2D(filters=F2, kernel_size=(f, f), strides=(1, 1), padding='same')(X)
X = keras.layers.BatchNormalization(axis=3)(X)
X = keras.layers.Activation('relu')(X)
# 塊 3
X = keras.layers.Conv2D(filters=F3, kernel_size=(1, 1), strides=(1, 1), padding='valid')(X)
X = keras.layers.BatchNormalization(axis=3)(X)
# 跳躍連線
X = keras.layers.Add()([X, X_shortcut])
X = keras.layers.Activation('relu')(X)
return X
def convolutional_block(X, f, channels, s=2):
'''
卷積塊--(卷積塊)--卷積塊
'''
F1, F2, F3 = channels
X_shortcut = X
# 主通路
# 塊1
X = keras.layers.Conv2D(filters=F1, kernel_size=(1, 1), strides=(s, s), padding='valid')(X)
X = keras.layers.BatchNormalization(axis=3)(X)
X = keras.layers.Activation('relu')(X)
# 塊2
X = keras.layers.Conv2D(filters=F2, kernel_size=(f, f), strides=(1, 1), padding='same')(X)
X = keras.layers.BatchNormalization(axis=3)(X)
X = keras.layers.Activation('relu')(X)
# 塊3
X = keras.layers.Conv2D(filters=F3, kernel_size=(1, 1), strides=(1, 1), padding='valid')(X)
X = keras.layers.BatchNormalization(axis=3)(X)
# 跳躍連線
X_shortcut = keras.layers.Conv2D(filters=F3, kernel_size=(1, 1),
strides=(s, s), padding='valid')(X_shortcut)
X_shortcut = keras.layers.BatchNormalization(axis=3)(X_shortcut)
X = keras.layers.Add()([X, X_shortcut])
X = keras.layers.Activation('relu')(X)
return X
# ===== ResNet-50 ===== #
IN_GRID = keras.layers.Input(shape=(256, 256, 3)) # 輸入256x256的RGB圖像
# 0填充
X = keras.layers.ZeroPadding2D((3, 3))(IN_GRID)
# 主通路
X = keras.layers.Conv2D(64, (7, 7), strides = (2, 2))(X)
X = keras.layers.BatchNormalization(axis=3)(X)
X = keras.layers.Activation('relu')(X)
X = keras.layers.MaxPooling2D((3, 3), strides=(2, 2))(X)
# 殘差塊1
X = convolutional_block(X, 3, [64, 64, 256])
X = identity_block(X, 3, [64, 64, 256])
X = identity_block(X, 3, [64, 64, 256])
# 殘差塊2
X = convolutional_block(X, 3, [128, 128, 512])
X = identity_block(X, 3, [128, 128, 512])
X = identity_block(X, 3, [128, 128, 512])
X = identity_block(X, 3, [128, 128, 512])
# 殘差塊3
X = convolutional_block(X, 3, [256, 256, 1024], s=2)
X = identity_block(X, 3, [256, 256, 1024])
X = identity_block(X, 3, [256, 256, 1024])
X = identity_block(X, 3, [256, 256, 1024])
X = identity_block(X, 3, [256, 256, 1024])
X = identity_block(X, 3, [256, 256, 1024])
# 殘差塊4
X = convolutional_block(X, 3, [512, 512, 2048])
X = identity_block(X, 3, [512, 512, 2048])
X = identity_block(X, 3, [512, 512, 2048])
# 全局均值池化
X = keras.layers.AveragePooling2D(pool_size=(1,1), padding='same')(X)
X = keras.layers.Flatten()(X)
# 輸出分類（按ImageNet為1000個分類）
OUT = keras.layers.Dense(1000, activation='softmax')(X)
# Create model
ResNet50 = keras.models.Model(inputs=IN_GRID, outputs=OUT)
# 編譯模型
opt = keras.optimizers.Adam(lr=0.001, decay=0.0)
ResNet50.compile(loss=keras.losses.categorical_crossentropy, optimizer=opt, metrics=['accuracy'])
# 輸出模型結構
keras.utils.plot_model(ResNet50, show_shapes=True, show_layer_names=False)
#
ResNet50.fit_generator(...) # 訓練模型
實驗
- 實驗了plain-18和plain-34，展示了退化問題。說明了退化問題不是因為梯度彌散，因為加入了BN。另外也不能簡單地增加疊代次數來使其收斂，增加疊代次數仍然會出現退化問題。
- 實驗了ResNet-18和ResNet-34不會出現退化問題，ResNet-34明顯表現的比ResNet-18和plain-34好，證明了殘差學習解決了隨網路深度增加帶來的退化問題。 而且同等深度的plain-18和ResNet-18，殘差網路更容易最佳化，收斂更快。
- 對於同等映射維度不匹配時，匹配維度的兩種方法，zero padding是參數free的，投影法會帶來參數。作者比較了這兩種方法的優劣。實驗證明，投影法會比zero padding表現稍好一些。因為zero padding的部分沒有參與殘差學習。實驗表明，將維度匹配或不匹配的同等映射全用投影法會取得更稍好的結果，但是考慮到不增加複雜度和參數free，不採用這種方法。
深層探究
作者探索的更深的網路。 考慮到時間花費，將原來的building block(殘差學習結構)改為瓶頸結構，如圖4。首端和末端的1x1卷積用來削減和恢復維度，相比於原本結構，只有中間3x3成為瓶頸部分。這兩種結構的時間複雜度相似。此時投影法映射帶來的參數成為不可忽略的部分（以為輸入維度的增大），所以要使用zero padding的同等映射。替換原本ResNet的殘差學習結構，同時也可以增加結構的數量，網路深度得以增加。生成了ResNet-50，ResNet-101，ResNet-152. 隨著深度增加，因為解決了退化問題，性能不斷提升。作者最後在Cifar-10上嘗試了1202層的網路，結果在訓練誤差上與一個較淺的110層的相近，但是測試誤差要比110層大1.5%。作者認為是採用了太深的網路，發生了過擬合。
圖4 深層探究
