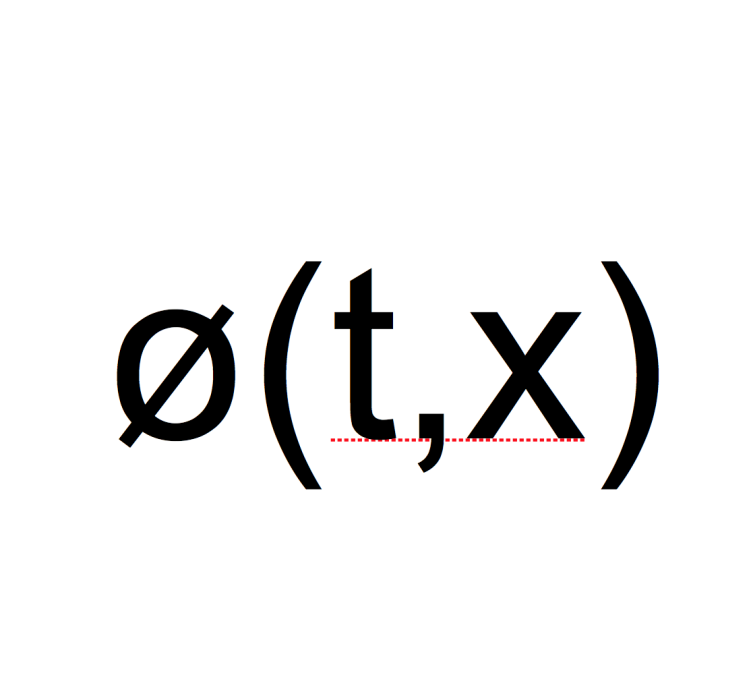殆周期函式

設ø：ℝ× X →X是一個拓撲動力系統，其中 X 是一個完備度量空間，其上的距離函式記為d(·,·)。給定x∈X，如果對任意的∈>0集合{t∈ℝ|對所有的s∈ℝ，都成立d(ø(s+t,x)，ø(s,x)) < ∈}在ℝ上都是相對稠密的，也就是說存在l= l(∈) > 0,使得ℝ上任意長度超過l的區間中都含有上述集合中的點，則稱點x是殆周期點(almost periodic point )，或稱ø(t,x)是一個殆周期運動。這種定義下的殆周期運動是一種回復性很強的運動，它等價於函式t→ø(t,x) 是R一X的一個殆周期函式(almost periodic point)。

基本介紹

• 中文名：殆周期運動
• 外文名：almost periodic motionx
• 適用範圍：數理科學
• 釋義：拓撲動力系統

定義

設ø：ℝ× X →X是一個拓撲動力系統，其中 X 是一個完備度量空間，其上的距離函式記為d(·,·)。給定x∈X，如果對任意的∈>0集合{t∈ℝ|對所有的s∈ℝ，都成立d(ø(s+t,x)，ø(s,x)) < ∈}在ℝ上都是相對稠密的，也就是說存在l= l(∈) > 0,使得ℝ上任意長度超過l的區間中都含有上述集合中的點，則稱點x是殆周期點(almost periodic point)，或稱ø(t,x)是一個殆周期運動。這種定義下的殆周期運動是一種回復性很強的運動，它等價於函式t→ø(t,x) 是R一X的一個殆周期函式(almost periodic point)。

由於定性理論通常是研究歐幾里得空間中的向量場，為了包含這類動力系統在這個定義中空間X通常不要求是緊緻的。即使向量場不能生成上述意義下的動力系統(例如，可能有些解曲線並不是對所有的時刻t都有定義),只要過x的解曲線對所有的時刻t都有定義，術語也可以定義。

動力系統

回復運動

[recurrent motion]：定性理論中一個名詞。

設ø是完備度量空間(X,d)上的一個拓撲動力系統。給定x∈X,如果對任意的∈>0,集合{t∈ℝ|d(ø(t,x),x)<∊}在R上都是相對稠密的，則稱ø(t,x)是一個回復運動，或稱點x是回復點(reccurrent point)。

如果x是回復的，則軌道Orb(x)的閉包是緊的，而且是一個極小集。

應該強調的是，這裡所說的回覆點與[抽象]動力系統中的“回復點”不同。這裡的回覆點在[抽象]動力系統中被稱為幾乎周期點(almost periodic point)或極小點(minimum point)。

泊松運動

[Poisson motion]：定性理論中的一個名詞。

設Ø是完備度量空間（X,d）上的一個拓撲動力系統。給定x∈X，如果x∈ω（x）∩ α（x），即存在兩個序列以及使得Ø，Ø，則稱Ø（t，x）是一個泊松運動或稱Ø（t，x）具有泊松穩定性（Poisson stability）。

應該強調的是，這裡所說的泊松穩定點在[抽象]動力系統中被稱為回復點。

具體說來，在[抽象]動力系統中，滿足x∈ω（x）的點x稱為正向回復點，滿足x∈α（x）的點x稱為負向回復點，而回復點則指的是正向回復點或負向回復點。而泊松穩定則指的是既正向回復又負向回復。

拉格朗日運動

[Lagrange motion]：設Ø是完備度量空間（X,d）上的一個拓撲動力系統，Ø（t，r）稱為一個拉格朗日運動或具有拉格朗日穩定性（Lagrange stability），如果軌道Orb（x）的閉包是緊緻的。