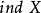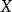歸納維數是對拓撲空間X定義的兩種維數,分別為小歸納維數ind(X)與大歸納維數Ind(X),它們的出發點都是基於空間維數與空間邊界維數的關係。首先點的維數為0,其邊界為空,因此定義ind(Φ)=Ind(Φ)=-1,其中ind表示小歸納維數,Ind表示大歸納維數。
對於空間X的任意點x及它的開鄰域U,存在x的另一個開鄰域V,使得V的閉包是U的子集且V的邊界的小歸納維數ind(boundary(V))≤n-1,則ind(X)≤n。進而,若ind(X)≤n-1不成立,則ind(X)=n。類似地有,對於空間X的任意閉集F及它的開鄰域U,存在F的另一個鄰域V,使得V的閉包是U的子集且V的邊界的小歸納維數Ind(boundary(V))≤n-1,則Ind(X)≤n。進而,若ind(X)≤n-1不成立,則ind(X)=n。
基本介紹
- 中文名:歸納維數
- 外文名:inductive dimension
- 所屬學科:數學(一般拓撲學)
- 分類:大歸納維數、小歸納維數
維數的發展,大歸納維數,小歸納維數,
維數的發展
維數是一個基本的拓撲概念。通俗地講,對於一個度量空間而言,維數是確定點或者點集位置所需要的參數的個數。對於向量空間來講,是空間中不相關的向量的最大個數。在直線上確定一個點的位置需要一個坐標,因此直線的維數是1;在平面上確定點的位置則需要兩個獨立的坐標參數,所以平面的維數記為2; 而我們現實所處的3維空間中的坐標個數為3,習慣上記為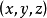 ,如果把點也當作空間,人們習慣上將其維數看作0。
,如果把點也當作空間,人們習慣上將其維數看作0。
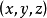
19世紀以後,人們開始逐漸研究維數高於3維的空間,比較典型的是物理學中將時間作為獨立坐標軸後建立的現實世界的4 維空間模型,即 ,使得在3 維空間中的物理定理和公式有了更為優美和簡潔的形式,也使得某些物理概念更為清晰和準確。隨後在不同的領域,高維空間的概念慢慢被人們接受與研究,在泛函中還研究了無窮維空間的性質。
,使得在3 維空間中的物理定理和公式有了更為優美和簡潔的形式,也使得某些物理概念更為清晰和準確。隨後在不同的領域,高維空間的概念慢慢被人們接受與研究,在泛函中還研究了無窮維空間的性質。

維數真正的定義源自龐加萊(Poincare),他指出若在曲線上標出一點,曲線通常就被分離成兩段,螞蟻從其中一段出發爬行,不接觸該點就無法進入另一段。因為曲線由點(0維) 分離,故曲線的維數大於0而為1。曲面就不能由點分成這樣兩塊,但可以用曲線分離,從而曲面的維數應高於曲線的維數。此外,立方體不能被點或曲線分離,但可以用曲面分離,故立方體的維數為3。這實際上為維數的定義提出了一種歸納的思路,隨後在20世紀初由布勞威爾(Brouwer)、切赫(Cech)、門傑(Menger) 和烏雷松(Urysohn)等人發展了上述思想以後,得到了兩種維數的定義,即大歸納維數與小歸納維數。之後,勒貝格(Lebesgue)和亞歷山德羅夫(Alexandrov)又從不同的角度分別定義了覆蓋維數和同調維數的概念。
大歸納維數
大歸納維數(large inductive dimension)是拓撲空間的一種維數,設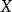 為正規空間,n表示非負整數,大歸納維數可如下確定:
為正規空間,n表示非負整數,大歸納維數可如下確定:
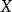
1. 若且唯若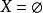 時,規定
時,規定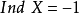 。
。
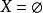
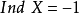
2. 若對於X的任意閉集A和包含A的X的任意開集V,存在X的開集U,使得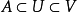 ,並且
,並且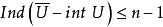 ,則規定
,則規定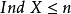 。
。
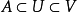
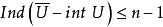
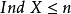
3. 若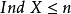 ,並且
,並且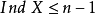 不成立,則規定
不成立,則規定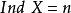 。
。
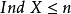
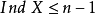
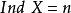
4. 若對於任意自然數n,不等式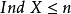 皆不成立,則規定
皆不成立,則規定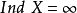 。
。
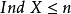
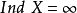
於是對於任意正規空間X確定的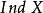 ,稱為
,稱為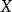 的布勞威爾-切赫維數或大歸納維數,若空間X與Y同胚,則
的布勞威爾-切赫維數或大歸納維數,若空間X與Y同胚,則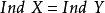 。
。
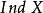
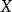
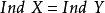
小歸納維數
小歸納維數(small inductive dimension)是拓撲空間的一種維數,設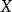 為正規空間,n表示非負整數,小歸納維數可如下確定:
為正規空間,n表示非負整數,小歸納維數可如下確定:
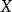
1. 若且唯若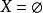 時,規定
時,規定 。
。
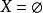

2. 若對於X的任意點x及x的任意鄰域V,存在x的開鄰域U,使得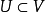 ,並且
,並且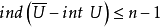 ,則規定
,則規定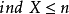 。
。
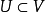
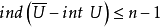
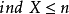
3. 若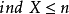 ,並且
,並且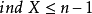 不成立,則規定
不成立,則規定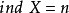 。
。
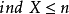
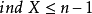
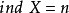
4. 若對於任意自然數n,不等式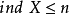 皆不成立,則規定
皆不成立,則規定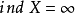 。
。
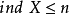
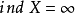
於是對於任意正規空間X確定的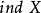 ,稱為
,稱為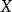 的門傑-烏雷松維數或小歸納維數,若空間X與Y同胚,則
的門傑-烏雷松維數或小歸納維數,若空間X與Y同胚,則 。
。