概念
兩種相關聯的變數,一種量變化,另一種量也隨著變化,如果這兩種相對應的比值一定,那么這兩個變數之間的關係就叫做正比例關係。用字母表示是
=k(一定)(k≠ 0)。
意義
滿足關係式y=k·x(k為一定量)的兩個變數,我們稱這兩個變數的關係成正
比例。顯然,若y與x成正比例,則y/x=k(k為
常量),反之亦然。
例如:在行程問題中,若速度一定時,則路程與時間成正比例;在工程問題中,若工作效率一定時,則工作總量與工作時間成正比例。
注意:k不能等於0。
相關聯繫
與反比例的關係如下:
相同之處
1、事物關係中都有兩個變數,一個定量。
2、在兩個變數中,當一個變數發生變化時,則另一個變數也隨之發生變化。
3、相對應的兩個變數的積或商都是一定的。
相互轉化
當反比例中的x值(自變數的值)也轉化為它的倒數時,由反比例轉化為正比例;當正比例中的x值(自變數的值)轉化為它的倒數時,由正比例轉化為反比例。
舉例
(1)正方形的周長與邊長 (比值:4)。
(2)同圓的周長與直徑 (比值:π)。
(3)購買的總價與購買的數量(比值:單價)。
(4)速度一定,路程和時間成正比例;時間一定,路程和速度成正比例。
解:aX=Y中,a不變,則 X與Y
成正比例。一個變數隨著另一個變數的變化而變化。
(5)圓的周長和半徑成正比例嗎?為什麼?
解:因為圓的周長除以圓的半徑=2π,所以圓的周長和半徑成正比例。
(6)易錯題:圓的面積(S):半徑(R)=πR
解:這個比例是錯誤的,它不屬於正比例。因為(S:R=πR)因為根據上面所說,比值須是一個不變的量,而比的前項和後項必須是可以變化的量,如果R變化,那比值也會變化,所以圓的面積與半徑不成正比例。
(7)易錯題:圓的面積(S):π=R·R(一定)
解:這是一個錯誤的比例,因為比值是不變的量,前項與後項應隨著一個的變化而變化,而在這裡,比值是個固定的量,而π也是一個固定的量,前項無法變化,這個比例就成了一個固定的比例,不符合上面所說的前項和後項必須是可以變化的量。
(6)易錯題:正方形的面積與邊長中, S:A=A
解:由上述可以看出:比值是個變數,它不能與比的任意一項相同,所以這個比例也不是正比例。
但如果圓的面積(S):(R·R) (R的平方)=π,這可看成一個正比例,它是S與(R·R)成正比例。
↑一種量
9
| | | | | | | | | ╱
|
8
| | | | | | | | ╱
| |
7
| | | | | | | ╱
| | |
6
| | | | | | ╱
| | | |
5
| | | | | ╱
| | | | |
4
| | | | ╱
| | | | | |
3
| | | ╱
| | | | | | |
2
| | ╱
| | | | | | | |
1
| ╱
| | | | | | | | |
除法
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
|
→一種量
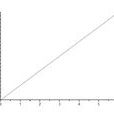
正比例的圖像是在一條過原點的射線上。
就是從統計表的橫坐標、縱坐標交匯處沿左下角到右上角的對角線發展,延伸至表格外,在這裡正比例的意義上它可以向下延伸,所以認為它是直線。
套用例子
例如:一輛汽車的最大速度為X千米/時,去A地需要Y小時,利用正比例可以計算去B地需要的時間。