正方形是特殊的平行四邊形之一。即有一組鄰邊相等,並且有一個角是直角的平行四邊形稱為正方形。正方形判定定理是幾何學裡用於判定一個四邊形是否為正方形的判定定理。判別正方形的一般順序為先說明它是平行四邊形;再說明它是菱形(或矩形);最後說明它是矩形(或菱形)。
基本介紹
- 中文名:正方形判定定理
- 外文名:A square judgement theorem
- 套用學科:幾何學
- 適用領域範圍:數理科學
- 定義:判定一個四邊形是否為正方形
- 性質:具有平行四邊形、矩形、菱形的一切性質。
正方形,判定定理,相關拓展,
正方形
定義:正方形是特殊的平行四邊形之一。即有一組鄰邊相等,並且有一個角是直角的平行四邊形稱為正方形。
性質:正方形具有平行四邊形、長方形、菱形的一切性質。
①對邊平行且相等。
②四條邊都相等。
③四個角都是直角。
④兩條對角線相等,互相垂直平分,且平分每組對角。
⑤正方形是軸對稱圖形,也是中心對稱圖形。
周長:正方形的周長等於它的邊長的4倍。若正方形的邊長為a,周長為C,那么C=4a。
例:一個正方形的邊長為4厘米,求這個正方形的周長。
解:C=4a=4×4=16(厘米)。
面積:
已知正方形的邊長為a,對角線長為d,則正方形的面積 。
。

判定定理
1、對角線互相垂直平分且相等的四邊形是正方形。
2、鄰邊相等且有一個內角是直角的平行四邊形是正方形。
3、有一組鄰邊相等的矩形是正方形。
4、有一個內角是直角的菱形是正方形。
5、對角線相等的菱形是正方形。
6、對角線互相垂直的矩形是正方形。
7、有三個內角為直角且有一組鄰邊相等的四邊形是正方形。
判別正方形的一般順序:先說明它是平行四邊形;再說明它是菱形(或矩形);最後說明它是矩形(或菱形)。
一個角為直角,並且一組鄰邊相等的平行四邊形,叫做正方形。如圖3-20的平行四邊形ABCD中,∠A為直角,AB=BC,那么平行四邊形ABCD就是正方形。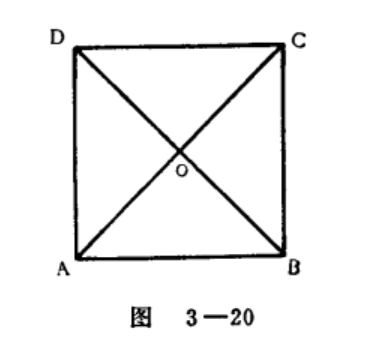

因為正方形是平行四邊形,也是矩形,又是菱形,所以它具有平行四邊形、矩形、菱形的一切性質。
相關拓展
1、正方形與平行四邊形、矩形、菱形的關係:
正方形是特殊的矩形和特殊的菱形,也就是說,正方形既是矩形又是菱形,還是平行四邊形,它們的包含關係。如圖:
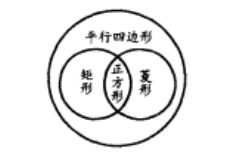
2、正方形的對稱性
正方形既是軸對稱圖形,又是中心對稱圖形,有四條對稱軸對稱軸的交點是對稱中心,如圖所示:
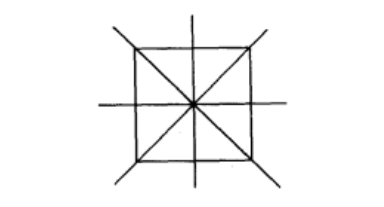
兩條對角線所在的直線和兩組對邊中點所確定的直線都是正方形的對稱軸。
3、正方形的兩條對角線把正方形分成四個全等的等腰直角三角形,如圖:
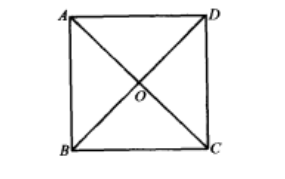
如圖,已知四邊形ABCD是正方形,對角線AC、BD相交於點O
求證:△ABO、△BOO、△CDO、△DAO是全等的等腰直角三角形
證明:∵四邊形ABCD是正方形,
∴AC=BD,AC⊥BD,
AO=BO=CO=DO.
∴△ABO、△BCO、△CDO、△DAO都是等腰直角三角形,
並且△ABO≌△BCO≌△CDO≌△DAO.