基本介紹
- 中文名:正多面角
- 外文名:regular polyhedral angle
- 所屬學科:數學(立體幾何)
- 簡介:面角、二面角都相等的凸多面角
- 性質:一種特殊的多面角
基本概念
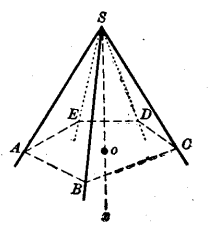
相關介紹
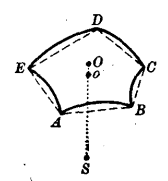
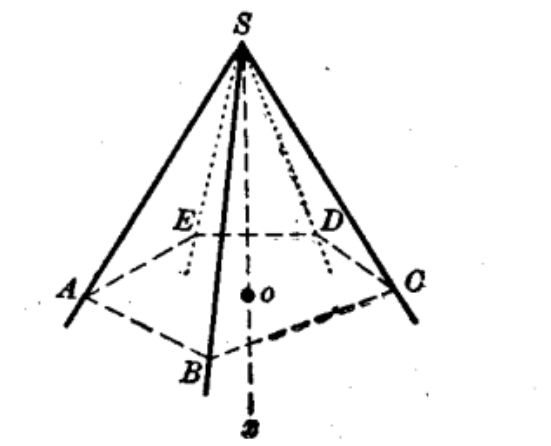


正多面角(regular polyhedral angle)是一種特殊的多面角,指所有面角相等,所有二面角也相等的凸多面角。凸多面角是一種多面角,將多面角的任何一個面伸展成為平面,如果其他各面都在這個平面的同側,則稱該多...
正多面體是凸多面體,其各面皆系全等正多邊形,且所有多面角均相等,正多面體中每一個頂點通過的棱數是相同的。歐幾里德證明,僅存在有五種正多面體:正四面體(圖1)、正六面休或正方體(圖2)、正八面體(圖3)、正十二面體(圖4)和...
我們可以想像到常用的手套,可以把兩隻手套排成對稱形,但是如果要把它的一隻套在另一隻上面,由於手心、手背以及五個指頭的順序不同,是不可能的。只有兩個面數相同的正多面角,它們既是成對稱(即鏡照相等),又是全等的。
正多面體 所謂正多面體,是指多面體的各個面都是全等的正多邊形,並且各個多面角都是全等的多面角。例如,正四面體(即正稜錐體)的四個面都是全等的三角形,每個頂點有一個三面角,共有三個三面角,可以完全重合,也就是說它們是全等...
等角多面體(equiangular polyhedron)是一種簡單多面體,指各多面角相等,且各面都是等角多邊形的多面體,這裡等角多邊形可能是正多邊形也可能是等角半正多邊形。例如,矩形是等角半正四邊形,長方體是等角多面體。基本介紹 等角多面體和等面...
鈍多面角是一種特殊的多面角,指以多面角的頂點為球心作單位球面,如果多面角在單位球面上截出的部分(球面多面形)的面積大於全球面面積的八分之一(即π/2),則稱該多面角為鈍多面角。性質 經過契約變換後重合的多面角稱為多面角的...
6.各側棱與底面的夾角都相等。7.相鄰兩個側面所組成的二面角都相等。8.正稜錐頂點處的多面角是正多面角。(4)記F為多面體的面數,多面體的面角之和為Σα,多面體的頂點數為V,則有以下表格:根據數據結論可推導出結論:
第四章 多面角和正多面體 §1.多面角 (1)三面角的不等量關係問題(723―732)(2)三面角的位置關係(733―738)(3)三面角的度量問題(739―751)(4)其它(752―756)§2.正多面體 (1)正多面體的一般問題(757―787)(...
