正則集(regular set)是集合論的一個重要概念。它是為避免出現悖論的奇特集合而引進的。
基本介紹
- 中文名:正則集
- 外文名:regular set
集合x是正則的,如果存在x的元素y,使得x和y沒有公共元素。
用符號表示為:x是正則集⇔(∃y∈x)(y∩x=∅)。
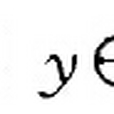
正則集(regular set)是集合論的一個重要概念。它是為避免出現悖論的奇特集合而引進的。
正則集(regular set)是集合論的一個重要概念。它是為避免出現悖論的奇特集合而引進的。集合x是正則的,如果存在x的元素y,使得x和y沒有公共元素。用符號表示為:x是正則集⇔(∃y∈x)(y∩x=∅)。...
,則稱𝑘為一個正則基數。事實上,任意滿足 的序數(即任意非奇異序數)一定是一個基數,因此正則基數也可以定義為等於它自己共尾度的序數。在ZFC中可以證明,任何後繼基數均為正則基數(這裡選擇公理是必須的)。另外,0和N₀是...
設T∈B(X),λ∈C如果λI一T有有界的逆運算元,則稱複數λ是運算元T的正則點;否則(即λI一T無有界逆運算元),稱λ為T為的譜點.記ρ(T)是T的全體正則點之集,σ(T)是T的譜,當λ∈ρ(T)時,稱運算元 為T的預解運算元(或預...
ρ(T)的余集C\ρ(T)稱為T的譜集,簡稱譜,記為σ(T')或Sρ(T)。性質 當X是巴拿赫空間時,任何線性運算元的正則集都是開集。進一步,當T'是有界時,ρ(T)和σ(T)都是非空的。線性運算元T的特徵值也稱為點譜,其全體記為σ...
1、正則集與正則集合運算運算元 Tilove根據點集拓撲學的原理,給出了正則集的定義。認為正則的幾何形體是由其內部點的閉包構成,即由內部點和邊界兩部分組成。對於幾何造型中的形體,規定正則形體是三維歐氏空間中的正則集合,因此可以將...
