基本介紹
- 中文名:正交對稱李代數的分解
- 外文名:decomposition of or-thogonal symmetric Lie algebra
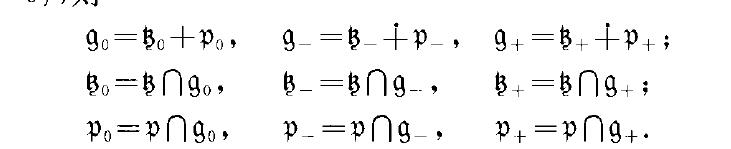
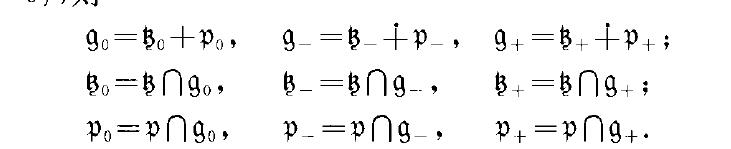
正交對稱李代數的分解,數學名詞。正交對稱李代數的分解,正交對稱李代數的直和分解一個有效正交對稱李代數(g}}}Q)可惟一地分解為。不變的歐幾里得型、緊型、非緊型理想9o}g-}9+的直和:g=90+9+①9一事實上g的基...
正交對稱李代數(orthogonal symmetric Lie al-gebra)實李代數的一種特徵子代數.實李代數g的對合自同構。的不動點集={XEgI X>=X}稱為。的特徵子代數.協是g的子代數,又稱(g,,Q)為對稱李代數.若由adFi生成g的線性變換的連通李群是緊緻的,則稱(g,,Q)為正交對稱李代數.若C(g>自= CO),則稱(g,,...
對稱空lei的全測地子流形(totally geodesicsubmanifold of symmetric spaces)對稱空間的一類特殊子流形。.設1 /1 =,對應的正交對稱李代數有分解g一協乾p.所以二處M的切空間T,M=}. M的子流形S在二處的切空間T萬_是p的子空間.S為M的全測地子流形若且唯若易是g的李三重系,即 [[弓,弓〕,弓〕...
第一個分解定理:單連通埃爾米特對稱空間可惟一地分解為一個n維復空間Cn、一個緊型埃爾米特對稱空間M一與一個非緊型埃爾米特對稱空間M+之積,其對應的有效正交對稱李代數有相應的分解.第二個分解定理:半單型埃爾米特對稱空間M可惟一地分解為不可約埃爾米特對稱空間之積,即 M=M,XMZX…X Mn,式中M是不可約埃爾...
decomposition the-orems of Riemannian symmetric spaces)刻畫黎曼對稱空間的基本定理.第一分解定理:單連通黎曼對稱空間M可惟一地分解為一個歐幾里得空間Mo,一個緊型單連通黎曼對稱空間M與一個非緊型黎曼對稱空間M+的積,即M=M} X M一X M十.M對應的有效正交對稱李代數(g,},a)有相應的分解(g,},a)=(g。
非緊型黎曼對稱空間一定是非緊的,且其截面曲率處處非正.非緊型黎曼對稱空間一定是單連通的.從而對應於一個非緊型正交對稱李代數只有惟一的黎曼對稱空間.非緊型正交對稱李代數(g,t},a>中之a'洽為g的嘉當對合,g=}乾p為嘉當分解.因此,非緊型黎曼對稱空間的分類實際上就是非緊實半單李代數的分類,這也是...
不可約黎曼對稱空間(irreducible Riemanniansymmetric space)最基本的黎曼對稱空間.若黎曼對稱空間M對應的正交對稱李代數(gr)>是半單的,即g為實半單李代數,則稱M為半單型的.若將g的伴隨模y限制於協上,則g為必模(ad辦9)> >是協模g的子模.若p是不可約的,則稱(gr)為不可約正交對稱李代數,M為不可約黎...
