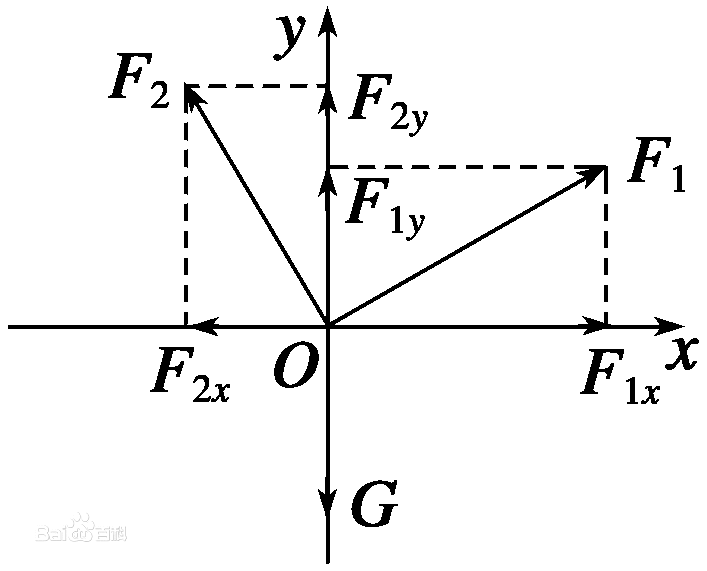正交分解是高中物理力學的一種求解方法。全稱為“力的正交分解”。
將一個力分解為Fx和Fy兩個相互垂直的分力的方法，叫作力的正交分解。從力的矢量性來看，是力F的分矢量；從力的計算來看，力的方向可以用正負號來表示，分量為正值表示分矢量的方向跟規定的正方向相同，分量為負值表示分矢量的方向跟規定的正方向相反。這樣，就可以把力的矢量運算轉變成代數運算．所以，力的正交分解法是處理力的合成分解問題的最重要的方法，是一種解析法．特別是多力作用於同一物體時。
它是力的合成的逆運算。
基本介紹
- 中文名：正交分解
- 外文名：orthogonal decomposition
- 套用：受力分析 等
- 領域：數學、物理學
- 全稱：力的正交分解
- 性質：力的合成的逆運算
- 套用：求合力
概述,求合力,目的與原則,典型例題,例1,例2,例3,運用關鍵,其他分解,
概述
插圖1.介紹：高中物理力學的一種求解方法。全稱為“力的正交分解”
2.定義：將一個力分解為Fx和Fy兩個相互垂直的分力的方法，叫作力的正交分解
從力的矢量性來看，是力F的分矢量；從力的計算來看，力的方向可以用正負號來表示，分量為正值表示分矢量的方向跟規定的正方向相同，分量為負值表示分矢量的方向跟規定的正方向相反．這樣，就可以把力的矢量運算轉變成代數運算．所以，力的正交分解法是處理力的合成分解問題的最重要的方法，是一種解析法．特別是多力作用於同一物體時。
3.它是力的合成的逆運算。
求合力
第一步，選定研究對象.並以質點的形式對進行表示。
第二步，對選定的研究對象進行受力分析。
正交分解
正交分解第三步，建立直角坐標系.一般來講在水平面內可以任意建立坐標系，但是在斜面上最好沿物體下滑的方向建立x軸，然後建立y軸。
第四步，分析加速度方向。必要時也可將加速度進行正交分解，以便於做題。
第五步，表達合外力。第六步，列出x方向，與y方向上的牛頓第二定律方程。第七步，若需其他方程，也要列出需要的方程，然後求解。
第八步，檢驗是否符合實際情況。（比如力為負的不可取）
目的與原則
把力沿著兩個經選定的互相垂直的方向分解叫力的正交分解法，在多個共點力作用下，運用正交分解法的目的是用代數運算公式來解決矢量的運算.在力的正交分解法中，分解的目的是為了求合力，尤其適用於物體受多個力的情況，物體受到F1,F2,F3…，求合力F時，可把各力沿相互垂直的x軸，y軸分解，則在x軸方向各力的分力分別為 F1x,F2x,F3x…，在y軸方向各力的分力分別為F1y,F2y,F3y….那么在x軸方向的合力Fx = F1x+ F2x+ F3x+ …，在y軸方向的合力Fy= F1y+ F2y+ F3y+….合力，設合力與x軸的夾角為θ，則.在運用正交分解法解題時，關鍵是如何確定直角坐標系，在靜力學中，以少分解力和容易分解力為原則；在動力學中，以加速方向和垂直加速度方向為坐標軸建立坐標，這樣使牛頓第二定律表達式為：F=ma。
典型例題
例1
物體放在粗糙的水平地面上，物體重50N，受到斜向上方向與水平面成30°角的力F作用，F = 50N，物體仍然靜止在地面上，如圖1所示，求：物體受到的摩擦力和地面的支持力分別是多少
解析：對F進行分解時，首先把F按效果分解成豎直向上的分力和水平向右的分力，對物體進行受力分析如圖2所示.F的效果可以由分解的水平方向分力Fx和豎直方向的分力Fy來代替.則：
由於物體處於靜止狀態時所受合力為零，則在豎直方向有：Fy=Fsin30° 則在水平方向上有：Fx=Fcos30°
例2
一物體放在傾角為θ的光滑斜面上，求使物體下滑的力和使物體壓緊斜面的力.
解析：使物體下滑的力和使物體壓緊斜面的力都是由重力引起的，把重力分解成兩個互相垂直的兩個力，如圖4所示，其中F1 為使物體下滑的力，F2為物體壓緊斜面的力，則：
點評：F1和F2是重力的分力，與重力可以互相替代，但不能共存.
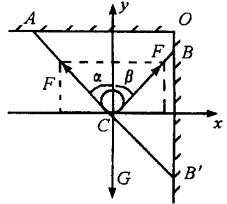
如圖5所示，拉力F作用在重為G的物體上，使它沿水平地面勻速前進，若物體與地面的動摩擦因數μ，當拉力最小時和地面的夾角θ為多大
解析：選取物體為研究對象，它受到重力G，拉力F，支持力N和滑動摩擦力f的作用,根據平衡條件有：
解得：
設，則，代入上式可得：
當時，，此時F取最小值.
拉力取最小值時，拉力與地面的夾角
點評：這是一個和數學最值知識相結合典型例題，同學們可以通過本題體會和總結用數學知識解決物理問題的方法，逐步建立數學物理模型.
例3
大小均為F的三個力共同作用在O點，F1,F2與F3之間的夾角均為60°，求合力.
⑴分別把各個力分解到兩個坐標軸上
⑶求出Fx和Fy的合力既是所求的三個力的合力
，則合力與F1的夾角為60°
點評：用正交分解法求共點力的合力的運算通常較為簡便，因此同學們要在今後學習中經常套用.
運用關鍵
在處理力的合成和分解問題時，我們常把力沿兩個互相垂直的方向分解，這種方法叫做力的正交分解法。這是一種很有用的方法，在運用時要注意以下幾點：
1.力是矢量F′在X軸Y軸上的分矢量F′x和F′y是矢量，分量為正值表示分矢量的方向跟坐標軸的方向相同，分量為負值表示分矢量的方向跟坐標軸的方向相反。
2．確定矢量正交分量的坐標軸，不一定是取豎直方向和水平方向。例如，分析物體在斜面上的受力情況，一般選取x軸與斜面平行，y軸與斜面垂直。坐標軸的選取是以使問題的分析簡化為原則。通常選取坐標軸的方法是：選取一條坐標軸與物體運動的加速度的方向相同（包括處理物體在斜面上運動的問題），以求使物體沿另一條坐標軸的加速度為零，這樣就可得到外力在該坐標軸上的分量之和為零，從而給解題帶來方便。
其他分解
矩陣的正交分解
矩陣的正交分解是指A分解為一個正交矩陣Q和一個對角可逆上三角矩陣R的乘積。
矩陣正交分解的套用
正交分解是先將線性方程組Ax=b的係數矩陣A分解為一個正交矩陣Q和一個對角可逆上三角矩陣R的乘積。然後通過求解上三角方程組Rx=Qb而求得原方程組的解，這種方法一般比三角分解法運算量大，但數值穩定性較好。
弧形的正交分解
以受力點為切點做圓弧的切線，再進行分解。
