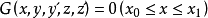歐拉-拉格朗日定理(Euler-Lagrange theorem)是把條件極值化歸為沒有約束條件的極值的一個定理。
基本介紹
- 中文名:歐拉-拉格朗日定理
- 外文名:Euler-Lagrange theorem
- 適用範圍:數理科學
簡介,具體內容,條件極值,
簡介
歐拉-拉格朗日定理是把條件極值化歸為沒有約束條件的極值的一個定理。
具體內容
歐拉-拉格朗日定理斷言:若函式(或曲線)y(x)在條件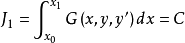 及邊界條件
及邊界條件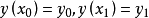 之下,給泛函
之下,給泛函 以極值,且若y(x)是滿足條件
以極值,且若y(x)是滿足條件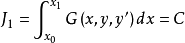 的泛函J的平穩函式,則存在這樣一個常數λ,使y(x)是泛函
的泛函J的平穩函式,則存在這樣一個常數λ,使y(x)是泛函 的平穩函式,其中H=F+λG。常數λ稱為歐拉-拉格朗日常數。
的平穩函式,其中H=F+λG。常數λ稱為歐拉-拉格朗日常數。
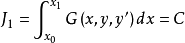
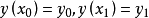

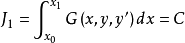

條件極值
條件極值是泛函J在某附加條件下的極值。
例如,泛函