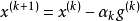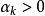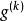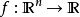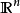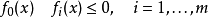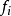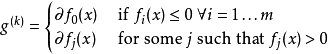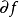次梯度法

次梯度法是求解凸函式最最佳化（凸最佳化）問題的一種疊代法。次梯度法能夠用於不可微的目標函式。當目標函式可微時，對於無約束問題次梯度法與梯度下降法具有同樣的搜尋方向。雖然在實際的套用中，次梯度法比內點法和牛頓法慢得多，但是次梯度法可以直接套用於更廣泛的問題，次梯度法只需要很少的存儲需求。然而，通過將次梯度法與分解技術結合，有時能夠開發出問題的簡單分配算法。

基本介紹

• 中文名：次梯度法
• 外文名：Subgradient method
• 套用：凸函式最最佳化問題
• 分類：最最佳化算法

基本次梯度算法

記 為定義在 上的凸函式。次梯度算法使用以下的疊代格式：

其中 表示函式 在 的次梯度. 如果 可微，他的次梯度就是梯度向量 有時， 不是函式 在 處的下降方向。因此採用一系列可能的 來追蹤目標函式的極小值點，即

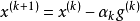
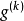
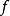
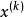
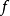
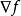
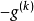
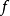
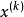
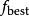
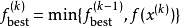
步長的選取

次梯度方法有許多可採用的步長。以下為5種能夠保證收斂性的步長規則：

1、恆定步長，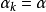

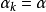
2、恆定間隔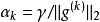，，得出。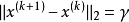

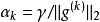
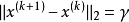
3、步長平方可加，但步長不可加，即步長滿足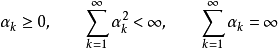

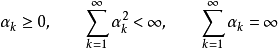
4、步長不可加但步長遞減，即步長滿足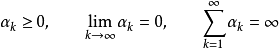

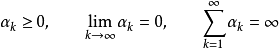
5、間隔不可加但間隔遞減，即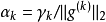，其中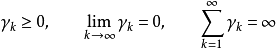

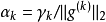
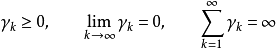
注意：上述步長是在算法執行前所確定的，不依賴於算法運行過程中產生的任何數據。這是與標準梯度下降法的顯著區別。

收斂結果

對於恆定間隔的步長以及恆定步長，次梯度算法收斂到最優值的某個鄰域，即

基本次梯度算法的性能較差，因此一般的最佳化問題並不推薦使用。

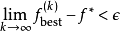
有約束最最佳化

投影次梯度算法

次梯度法的一個擴展版本是投影次梯度法，該方法用於求解有約束最最佳化問題：最小化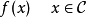,其中 C為凸集。投影次梯度算方法的疊代公式為:

其中P是在C的投影，是在點處的次梯度。

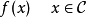
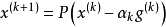
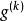
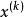
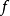
一般約束問題

次梯度法可擴展到求解求解不等式約束問題，最小化，其中為凸函式。該算法與無約束最佳化問題具有相同的形式：

其中，是步長，是目標函式或約束函式在 x處的次梯度

其中是f的次微分。如果當前點為可行點，算法採用目標函式的次梯度，否則採用任一違反約束的函式的次微分。