橢球偏心率是用來描述旋轉橢球形狀和大小的基本參數,包括橢圓扁率、橢圓的第一偏心率和橢圓的第二偏心率,它們都是反映橢球體扁平程度的參數(或稱元素)。
基本介紹
- 中文名:橢球偏心率
- 外文名:Eccentricity of Elliopsoid
- 適用學科:測繪科學與技術
- 套用領域:大地測量學
定義,性質,套用,
定義
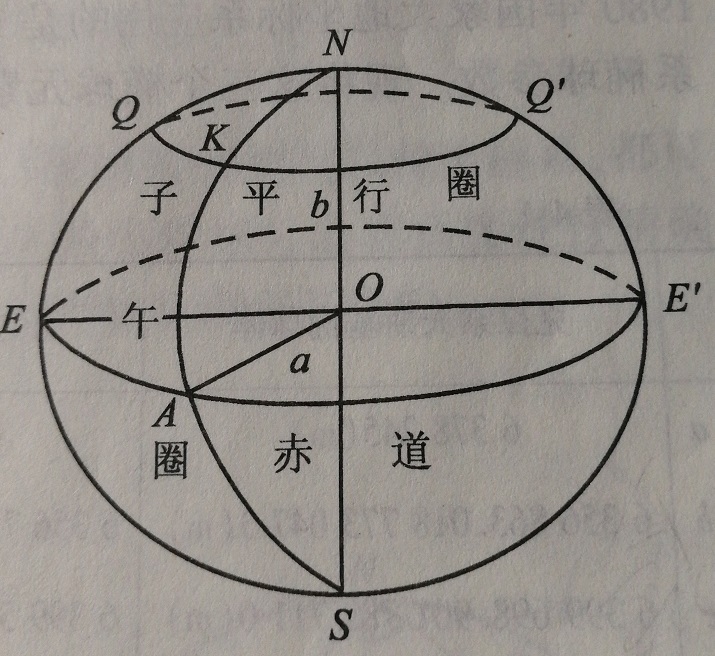
在控制測量中,用來代表地球的橢球叫做地球橢球。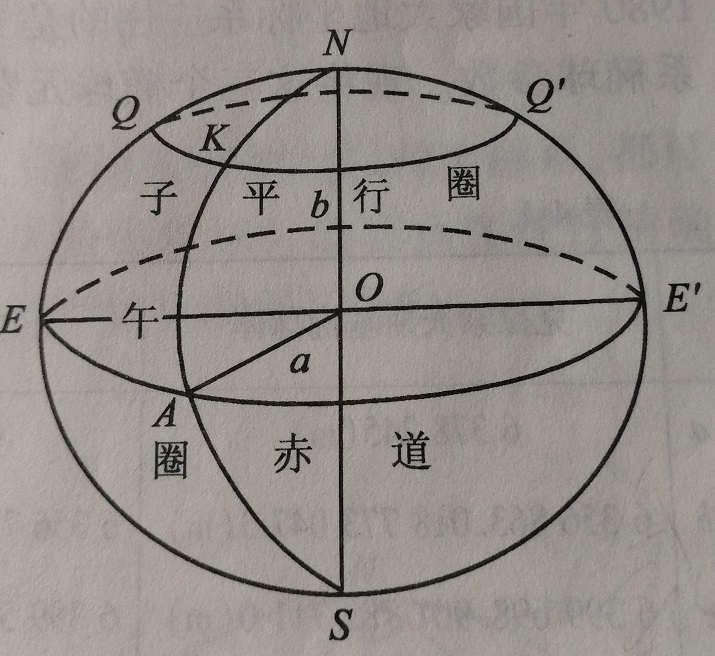 圖1 旋轉橢球
圖1 旋轉橢球
 圖1 旋轉橢球
圖1 旋轉橢球地球橢球是經過適當選擇的旋轉橢球。旋轉橢球是橢圓繞其短軸旋轉而成的幾何形體。在圖1中,O是橢球中心,NS為旋轉軸,a為長半軸,b為短半軸。包含旋轉軸的平面與橢球面相截所得的橢圓,叫子午圈(或經圈,或子午橢圓),如NKAS。旋轉橢球面上所有的子午圈的大小都是一樣的。垂直於旋轉軸的平面與橢球面相截所得的圓,叫平行圈(或緯圈),如QKQ'。通過橢球中心的平行圈,叫赤道,如EAE'。赤道是最大的平行圈,而南極點、北極點是最小的平行圈。
旋轉橢球的形狀和大小是由子午橢圓的五個基本幾何參數(或稱元素)來決定的,它們是:
橢圓的長半軸

橢圓的短半軸

橢圓的第一偏心率

橢圓的第二偏心率

橢圓的扁率

其中:a,b稱為長度元素;扁率α反映了橢球體的扁平程度,如當a=b時,α=0,橢球變為球體;當b減小時,α增大,則橢球體變扁;當b=0時,α=1,則變為平面。因此α值介於1和0之間。
偏心率e和e'是子午橢圓的焦點離開中心的距離與橢圓半徑之比,它們也反映橢球體的扁平程度,偏心率越大,橢球越扁,其數值恆小於1。
性質
決定旋轉橢球的形狀和大小,只需知道五個參數中的兩個參數就夠了,但其中至少有一個長度元素(如a或b),通常習慣於用a,e2或a,e'2或a,α,因為其中包含一個小於1的量,便於級數展開。
為簡化書寫,還常引入以下符號:


式中:B是大地緯度,c有明確的幾何意義,它是極點處的子午線曲率半徑。
套用
傳統大地測量利用天文大地測量和重力測量資料推求地球橢球的幾何參數。19世紀以來,已經求出許多地球參數,比較著名的有貝塞爾橢球(1841年),克拉克橢球(1866年),海福特橢球(1910年)和克拉索夫斯基橢球(1940年)等。20世紀60年代以來, 空間大地測量學的興起和發展,為研究地球形狀和引力場開闢了新途徑。國際大地測量和地球物理聯合會(IUGG)已推薦了更精密的橢球參數,比如第16屆IUGG大會(1975年)推薦的1975年國際橢球參數等。新中國成立以來,我國建立1954年北京坐標系套用的是克拉索夫斯基橢球;建立1980年國家大地坐標系套用的是1975年國際橢球;而全球定位系統(GPS)套用的是WGS-84系橢球參數。現將這三個橢球元素值列於下表。
克拉索夫斯基橢球體 | 1975國際橢球體 | WGS-84橢球體 | 2000中國大地坐標系 (CGCS2000) | |
a | 6378245(m) | 6378140(m) | 6378137(m) | 6378137(m) |
b | 6356863.0187730473(m) | 6356755.2881575287(m) | 6356752.3142(m) | 6356752.3141(m) |
c | 6399698.9017827110(m) | 6399596.6519880105(m) | 6399593.6258(m) | 6399752.314(m) |
e2 | 0.006693421622966 | 0.006694384999588 | 0.00669437999013 | 0.00669438002290 |
e'2 | 0.006738525414683 | 0.006739501819473 | 0.00673949674227 | 0.00673949677548 |
α | 1/298.3 | 1/298.257 | 1/ 298.257223563 | 1/298.257222101 |