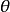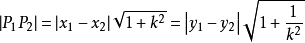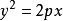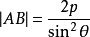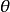橢圓弦長公式

橢圓弦長公式是一個數學公式，關於直線與圓錐曲線相交求弦長，通用方法是將直線y=kx+b代入曲線方程，化為關於x(或關於y)的一元二次方程，設出交點坐標，利用韋達定理及弦長公式求出弦長。

設而不求的思想方法對於求直線與曲線相交弦長是十分有效的，然而對於過焦點的圓錐曲線弦長求解利用這種方法相比較而言有點繁瑣，利用圓錐曲線定義及有關定理導出各種曲線的焦點弦長公式就更為簡捷。

基本介紹

• 中文名：橢圓弦長公式
• 方法：解析法
• 領域：解析幾何

釋義

關於直線與圓錐曲線相交求弦長，通用方法是將直線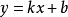 代入曲線方程，化為關於x(或關於y)的一元二次方程，設出交點坐標，利用韋達定理及弦長公式 求出弦長，這種整體代換，設而不求的思想方法對於求直線與曲線相交弦長是十分有效的，然而對於過焦點的圓錐曲線弦長求解利用這種方法相比較而言有點繁瑣，利用圓錐曲線定義及有關定理導出各種曲線的焦點弦長公式就更為簡捷。

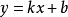
用極坐標方法

橢圓極坐標方程是：

其中e是橢圓離心率，p是焦點到對應準線的距離， 是弦與x軸所夾的角度

所以你要求的那個弦長就是

橢圓弦長公式

　若直線過焦點並知道傾斜角，則還可以使用

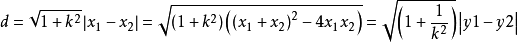
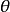
推導

設直線y=kx+b
代入橢圓的方程可得：x²/a²+ (kx+b)²/b²=1，
設兩交點為A、B，點A為（x1,y1)，點B為(x2,y2)
則有AB=√ [(x1-x2)²+(y1-y2)²]
把y1=kx1+b.y2=kx2+b分別代入,
則有：
AB=√ [(x1-x2)²+(kx1-kx2)²
=√ [(x1-x2)²+k²(x1-x2)²]
=│x1-x2│ √ (1+k²)　同理可以證明：弦長=│y1-y2│√[(1/k²)+1]

直線和橢圓的交點（默認一定存在交點，且直線 A!=0，B!=0;）

直線：Ax+By+C=0;

橢圓：x^2/a^2+y^2/b^2=1;

求直線和橢圓的交點：

(B^2+(A^2*a^2)/b^2)*y^2 + 2*B*C*y+C^2-A^2*a^2=0;

令m=(B^2+(A^2*a^2)/b^2);

n=2*B*C;

p=C^2-A^2*a^2;

令m1=(A^2+(B^2*b^2)/a^2);

n1=2*AC;

p1=C^2-B^2*b^2;

得到y=(-n±√(b^2-4*m*p))/2*m;

當y=(-n-√(b^2-4*m*p))/2*m;x=(-n1-√(b1^2-4*m1*p1))/2*m1

當y=(-n+√(b^2-4*m*p))/2*m;x=(-n1+√(b1^2-4*m1*p1))/2*m1

延伸

此公式適用於所有圓錐曲線（橢圓、雙曲線和拋物線）

橢圓：

(1)焦點弦:A(x1,y1),B(x2,y2),AB為橢圓的焦點弦，M(x,y)為AB中點，則L=2a±2ex

(2)設直線；與橢圓交於P1(x1,y1),P2(x2,y2),且P1P2斜率為k，則

雙曲線：

(1)焦點弦:A(x1,y1),B(x2,y2),AB為雙曲線的焦點弦，M(x,y)為AB中點，則l=-2a±2ex

(2)設直線；與雙曲線交於P1(x1,y1),P2(x2,y2),且P1P2斜率為k，則

同上

拋物線：

(1)焦點弦：已知拋物線,A(x1,y1),B(x2,y2),AB為拋物線的焦點弦，則

或{為弦AB的傾斜角}

(2)設直線；與拋物線交於P1(x1,y1),P2(x2,y2),且P1P2斜率為k，則同上