機器人運動學包括正向運動學和逆向運動學,正向運動學即給定機器人各關節變數,計算機器人末端的位置姿態; 逆向運動學即已知機器人末端的位置姿態,計算機器人對應位置的全部關節變數。
基本介紹
- 中文名:機器人運動學
- 外文名:robot kinematics
- 分類:計算機 機器人
- 相關:機器人動力學
- 包括:正向運動學 逆向運動學
- 簡稱:DKP IKP
- 變數:位置姿態 關節變數
簡介
位姿描述
表示




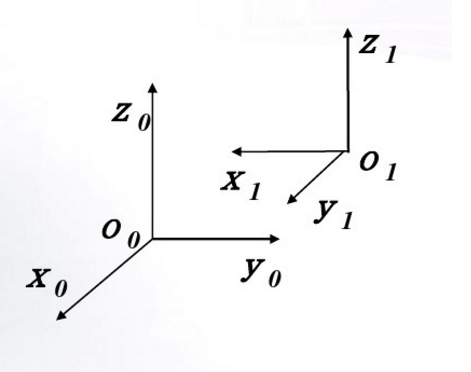

坐標
運動學方程
概念



舉例



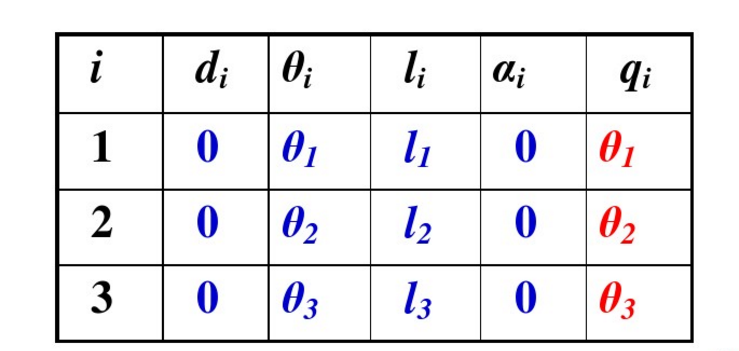
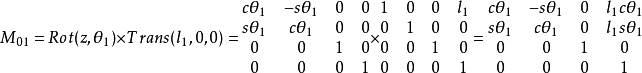


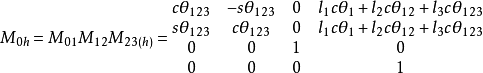
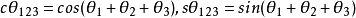

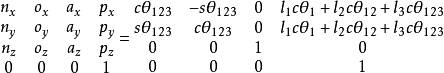




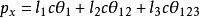


機器人運動學包括正向運動學和逆向運動學,正向運動學即給定機器人各關節變數,計算機器人末端的位置姿態; 逆向運動學即已知機器人末端的位置姿態,計算機器人對應位置的全部關節變數。













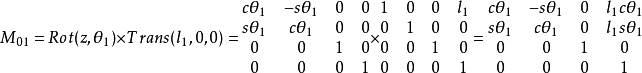


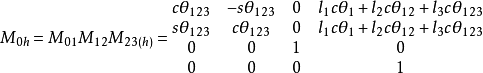
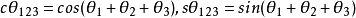

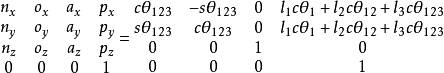




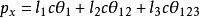

機器人運動學包括正向運動學和逆向運動學,正向運動學即給定機器人各關節變數,計算機器人末端的位置姿態; 逆向運動學即已知機器人末端的位置姿態,計算機器人對應位置...
機器人學——運動學、動力學與控制 中國科學院機械工程系列規劃教材 宋偉剛 編著 科學出版社 2007年10月出版 定價:35.00 語種:中文 標準書號:978-7-03-020176...
機器人動力學是對機器人機構的力和運動之間關係與平衡進行研究的學科。機器人動力學是複雜的動力學系統,對處理物體的動態回響取決於機器人動力學模型和控制算,主要...
機械運動學 拼音題名 責任者 華文廣編著 其他責任者 出版者 商務印書館[發行者] 出版地點 [上海] 出版時間 民國35[1946] 載體形態 343頁 叢編項 主題詞 ...
正向運動學是指採用一個機器人的運動方程,以從該關節參數指定的值計算所述端部執行器的位置。機器人的運動學方程用在機器人,計算機遊戲和動畫。相反的過程,計算該...
機器人運動學線上標定技術1 作者: 杜廣龍 張平 責編: 劉鋒 詹志青 出版日期:2016年8月 裝幀: 簡裝 ISBN: 978-7-5623-4902-0 開本: 16 開 版次: 1-1 ...
這種運動方式在運動學中有過相關的描述。由一個目標點去確定目標的運動,最後確定整個物體的運動。反向運動學操作 編輯 機器人學和三維動畫...
全面介紹了機器人建模與控制研究中所涉及的基本概念、算法和有代表性的結果,特別是控制方法的介紹更具全面性。全書共3章,分別是:機器人運動學,機器人動力學,機器...
2.4運動副及自由度422.4.1運動副及其分類422.4.2運動副與關節機構432.4.3關節及其分類432.4.4與自由度的關係432.4.5機器人運動副(關節)符號43...
機械動力學(dynamics of machinery)是機械原理的主要組成部分。研究機械在運轉過程中的受力、機械中各構件的質量與機械運動之間的相互關係,是現代機械設計的理論基礎...
運動學和動力學、系統結構、感測技術、控制技術、行動規劃和套用工程等。機器人學發展歷程 編輯 我國的機器人學科形成較晚,1985年前後在幾個一級學會下設立了機器...
機器人機械設計是機器人技術的一個重要方面。機器人機械設計與機器人伺服控制密切相關。本書圍繞機器人機械設計的特點展開,內容包括:導論、機器人運動學設計和分析、...
素質體育機器人運動教育基地,是由中國機器人運動委員會及其各省、自治區、直轄市分支機構,與大、中、國小及培訓機構建立合作,發揮雙方優勢,共同培養機器人教育、機器...
這裡的主要焦點是自我複製的機器系統。最重要的是,我們關心的是運動的自我複製的機器:系統中,實際的物理對象,而不是單純的信息模式,進行自己的複製。在20世紀50...
主要研究機器人的運動和動力分析、設計理論、方法及其套用,包括串聯和並聯柔性機器人動力學分析、柔性冗餘度機械臂振動控制、柔性並聯機器人冗餘驅動規劃、多柔性機器人...
此外,根據機械手運動和工作的要求,如管路、冷卻裝置、行程定位裝置和自動檢測裝置等,一般也都裝在手臂上。所以手臂的結構、工作範圍、承載能力和動作精度都直接影響...
根據機械原理,機構具有確定運動時所必須給定的獨立運動參數的數目(亦即為了使機構的位置得以確定,必須給定的獨立的廣義坐標的數目),稱為機構自由度(degree of ...
而複雜機械就是由兩種或兩種以上的簡單機械構成。通常把這些比較複雜的機械叫做機器。從結構和運動的觀點來看,機構和機器並無區別,泛稱為機械。...
機械傳動在機械工程中套用非常廣泛,主要是指利用機械方式傳遞動力和運動的傳動。分為兩類:一是靠機件間的摩擦力傳遞動力與摩擦傳動,二是靠主動件與從動件嚙合或...
英國工人以破壞機器為手段反對工廠主壓迫和剝削的自發工人運動。首領稱為盧德王,故名。相傳,萊斯特郡一個名叫盧德的工人,為抗議工廠主的壓迫,第一個搗毀織襪機。...
本課程使學生掌握常用機構,具有分析機械運動和動力性能的能力;掌握通用機械零件的知識,具有分析、選用和設計機械零部件及機械傳動裝置的能力和查閱、運用有關資料的...
機械能動能 物體由於運動而具有的能叫做動能,通常被定義成使某物體從靜止狀態至運動狀態所做的功。它的大小是運動物體的質量和速度平方乘積的二分之一。一切運動的...
機器通常是通過它將動力機產生的動力和運動傳遞給機器的工作部分。設定傳動是因為:機器工作部分所要求的速度和轉矩與動力機的不一致;有的機器工作部分常需要改變速度...
