模糊聯想記憶(Fuzzy Associative Memory,簡稱FAM)是通過一定的對應關係將一個論域中的模糊子集映射到另一個論域中,即要將一個立方體映射到另一個立方體,這種映射關係叫做“聯想記憶”,在模糊系統里具體稱為模糊聯想記憶。
基本介紹
- 中文名:模糊聯想記憶
- 外文名:fuzzy associative memory
- 簡稱:FAM
- 學科:控制科學與工程
- 提出者:Kosko
- 時間:1991年
基本概念
模糊聯想記憶模型
















模糊聯想記憶推理機


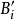






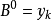









模糊聯想記憶與模糊關係方程

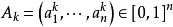



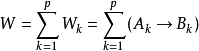













模糊聯想記憶(Fuzzy Associative Memory,簡稱FAM)是通過一定的對應關係將一個論域中的模糊子集映射到另一個論域中,即要將一個立方體映射到另一個立方體,這種映射關係叫做“聯想記憶”,在模糊系統里具體稱為模糊聯想記憶。


















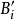






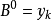










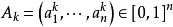



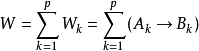












模糊聯想記憶(Fuzzy Associative Memory,簡稱FAM)是通過一定的對應關係將一個論域中的模糊子集映射到另一個論域中,即要將一個立方體映射到另一個立方體,這種映射...
自適應模糊聯想記憶,是通過一定的對應關係將一個論域中的模糊子集映射到另一個論域中,即要將一個立方體映射到另一個立方體,使這種映射關係與所處理數據的統計...
第八章 模糊神經網路 8.1模糊神經元及模糊神經網路 8.2模糊聯想記憶 8.3模糊極小―極大神經網路 8.4模糊關係神經網路 8.5模糊Hopfielld神經網路 8.6模糊推理的基...
第十章建立廣義模糊矩陣的極限理論。第十一章討論模糊矩陣方程。第四部分是全書的最後兩章,討論模糊矩陣理論的套用問題。其中,第十二章詳細介紹了模糊雙向聯想記憶...
(3)徐蔚鴻,宋孌姣等,訓練模式對的攝動對模糊雙向聯想記憶網路的影響和控制,計算機學報,2006,29(2):337~344(EI收錄),一級期刊...
§2.9 雙向聯想記憶(BAM)網路§2.10 模糊聯想記憶(FAM)網路習題第三章 徑向基函式網路§3.1 徑向基函式(RBF)§3.2 徑向基函式參數的選取...
二 模糊神經網路三 模糊BP網路四 模糊聯想記憶第四節 模糊聚類分析第五節 模糊c—均值算法第六節 模糊模式識別技術在故障診斷中的套用...
7.6幾種常見的模糊神經網路7.6.1模糊聯想記憶網路7.6.2模糊認知映射網路7.7小結習題與思考題第8章神經控制中的遺傳進化訓練8.1生物的遺傳與進化...
