基本介紹
- 中文名:模糊化
- 外文名:fuzzification
- 領域:自動化控制
- 釋義:將確定值轉換為相應的模糊變數值
- 相關概念:隸屬度函式
- 模糊化方法:分檔模糊集法、隸屬度值法等
基本信息
主要方法
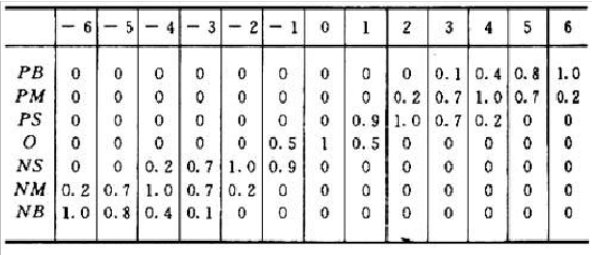


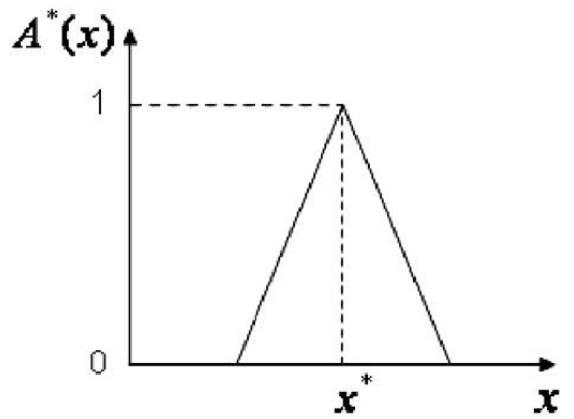
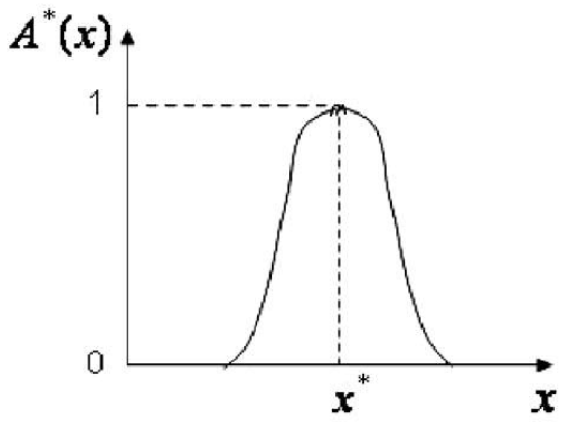

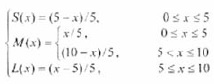
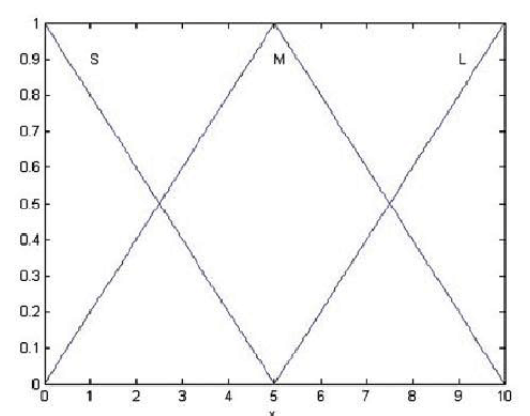
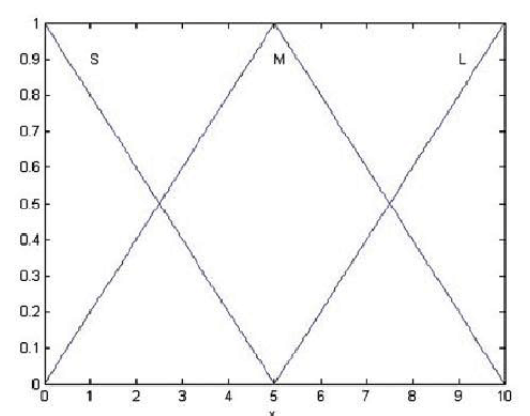









模糊化是實現模糊控制的一個重要環節,模糊化是將模糊控制器輸入量的確定值轉換為相應的模糊語言變數值的過程,而模糊語言變數值是一個模糊集合,所以模糊化方法應給出從精確量到模糊集合的轉變方法。常見的模糊化方法有分檔模糊集法、輸...
去模糊化是將推論所得到的模糊值轉換為明確的控制訊號,做為系統的輸入值。去模糊化是模糊推理機中重要的一步,也稱解模糊化。去模糊化的方法有很多種,最常用的有最大隸屬度法,重心法和加權平均法。相關定義 去模糊化:去模糊化是...
模糊化運算元(operator for fuzziness)是一種運算元,是改變單詞的模糊程度的一種運算元。它是這樣一個詞,放在某個單詞前面可使這個單詞的意義更加模糊,比如“大概”、“近似”等,一般可用一個模糊相似關係(即自反、對稱的模糊關係)來表示,...
模糊推理引擎是模糊系統的核心,它可以藉由近似推理或模糊推理的進行,來仿真人類的思考決策模式,以達到解決問題的日地。去模糊化機構 將經過模糊推理之後產生的結淪,轉換為一明確數值的過程,我們稱之為“去模糊化”。由於不同的模糊...
TSK模糊模型屬於模糊系統中的一種,模糊邏輯系統一般由模糊化、規則庫、模糊推理、輸出四部分組成,它的核心是模糊推理。TSK模糊系統是由Takagi、Sugeno和Kang提出的,該系統具有很好的非線性逼近能力,被廣泛運用到系統辨識、模式識別、圖像...
模糊PID(Fuzzy PID)是PID算法與模糊控制理論相結合的一種控制理論。控制器 通常,對於溫度控制的理解,是覺得其技術成熟且改變不大。有一些工業的套用(如,注塑工業),不僅對時間進行精確的控制,而且在當設定值改變時,對於快速加溫...
而模糊行銷的提出是筆者近幾年從事實踐的產物,是行銷“人”本身的思想產物。所謂模糊行銷就是倡導一種平衡,猶如武術中的太極,講究借力打力,四兩撥千斤的巧勁,而不是胡蘿蔔加大棒的蠻勁。內容 模糊化 現在企業在選擇目標市場上,絕...
那么我們完全可以用1*0.3+2*0.7+3*0.0=1.7來表示它,當然這個公式也不一定是這樣的,這個公式的設計是系統模糊化和精確化的一個過程,讀者也可參見相關文獻理解。但就1.7這個數字而言,可以說明,目前6°的角度偏差處於小和中...
“活性”問題歸根到底又是模糊識別、模糊分析和模糊綜合評判等思維整合機制問題; 人類認識有一個從巨觀原理到微觀機制轉化的過程; 模糊化思維需要模糊數學、人體科學、資訊理論、控制論、系統論以及人工智慧等學科發展到一定程度,為模糊認識...
模糊控制器包括四部分:(1)模糊化。主要作用是選定模糊控制器的輸入量,並將其轉換為系統可識別的模糊量,具體包含以下三步:第一,對輸入量進行滿足模糊控制需求的處理;第二,對輸入量進行尺度變換;第三,確定各輸入量的模糊語言取值...
式中u為一個模糊量;為了對被控對象施加精確的控制,還需要將模糊量u進行非模糊化處理轉換為精確量:得到精確數字量後,經數模轉換變為精確的模 擬量送給執行機構,對被控對象進行一步控制;然後,進行第二次採樣,完成第二步控制,...
ANFIS是一種基於Takagi-Sugeno模型的模糊推理系統,它將模糊控制的模糊化、模糊推理和反模糊化3個基本過程全部用神經網路來實現,利用神經網路的學習機制自動地從輸入輸出樣本數據中抽取規則,構成自適應神經模糊控制器,通過離線訓練和線上...
本書由淺入深地論述了模糊邏輯控制原理、模糊控制器的結構、控制規則的形式、模糊推理以及反模糊化等基本理論;從傳統控制工程設計出發,將傳統控制理論套用到模糊控制器的設計過程中;介紹了建立模糊控制系統仿真模型的方法及用MATLAB建立...
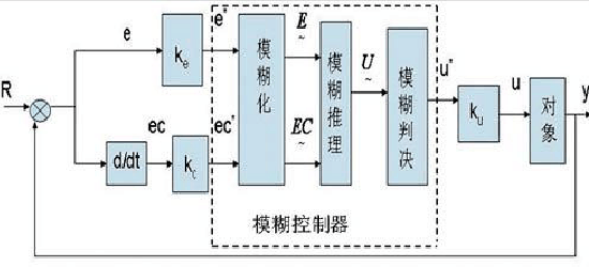
因此利用人的智力模糊地進行系統控制的方法就是模糊控制。如圖1所示,模糊控制器的基本結構包括知識庫、模糊推理、輸入量模糊化、輸出量精確化四部分。(1)知識庫 知識庫包括模糊控制器參數庫和模糊控制規則庫。模糊控制規則建立在語言變數...
模糊控制器包括四部分:(1)模糊化。主要作用是選定模糊控制器的輸入量,並將其轉換為系統可識別的模糊量,具體包含以下三步:第一,對輸入量進行滿足模糊控制需求的處理;第二,對輸入量進行尺度變換;第三,確定各輸入量的模糊語言取值...
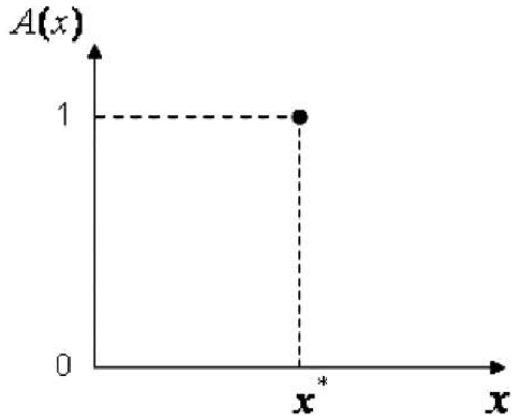
若在FAM系統中有m條規則,輸入為一個P維的模糊矢量A(通常輸入為確切的數值,需經模糊化處理)。它不同程度地並行激活相應的FAM規則F,並得到輸出B′。這樣,m條規則可能產生m個子結論B′₁,B′₂…,B′ₘ。將m個子結論按下...
同一個模糊控制規則庫,對基本論域的模糊劃分不同,控制效果也不同。模糊控制器 如圖1所示,模糊控制器的基本結構包括知識庫、模糊推理、輸入量模糊化、輸出量精確化四部分。(1)知識庫 知識庫包括模糊控制器參數庫和模糊控制規則庫。...
模糊尋優 給定方案集及各種目標函式和限制條件以後,尋求最優方案便成了一個最佳化問題。若目標函式或約束條件是模糊的,這時的最最佳化就稱為模糊尋優。目標函式模糊化的一種途徑是以模糊數作為目標函式值,通過模糊數的分析、運算來尋求條件...
模糊聯想記憶推理機 由FAM學習網路得到的規則可供FAM推理機進行推理。如圖1所示,若在FAM系統中有m條規則,輸入為一個P維的模糊矢量A(通常輸入為確切的數值,需經模糊化處理)。它不同程度地並行激活相應的FAM規則 ,並得到輸出 ...
