標準分，是一種由原始分推導出來的相對地位量數，它是用來說明原始分在所屬的那批分數中 的相對位置的。考生在接受測驗後，按照評分標準對其作答反應直接評出來的分數，叫原始分。
原始分反映 了考生答對題目的個數，或作答正確的程度。但是，原始分一般不能直接反映出考生間差異 狀況，不能刻劃出考生相互比較後所處的地位，也不能說明考生在其他等值測試上應獲得什 么樣的分值。
基本介紹
概述,簡介,計算,高考標準分,制度內容,理解使用,目的,使用,相關說明,
概述
簡介
導出分是在原始分的基礎上，按一定的規則推導出來的，其目的就是進一步解決原始分所沒 有解決的問題，或者說，就是為了更好、更科學地解釋分數的含義，進行分數的組合，實現 分數的等值化。這種把原始分數轉化為導出分的過程，稱作分數轉換。導出分的種類有很多 ，最常用的是百分等級和標準分數。
計算
Z=(X-X_bar)/S
式中，X為原始分數，X_bar為原始分的平均數，S為原始分的標準差。
Z分數是以一批分數的平均數作為參照點，以標準差作為單位表示距離的。它由正負號和絕 對數值兩部分組成，正負號說明原始分是大於還是小於平均數，絕對數值說明原始分距離平 均分數的遠近程度。一批分數全部轉換成Z分數後，它們的整個分布形態並沒有發生改變。Z 分數準確地刻劃了一個分數在一批分數中的相對位置，但是，由於Z分數有負值，常帶有小 數，不易被人理解和套用。因此人們在Z分數的基礎上進一步轉換，從而發展起了一系列其 他形式的標準分。轉換通式為：
Z′=αZ+β
式中，Z′為其他形式的標準分，β為基準分，一般等於原始分的平均分X_bar，α是擴大係數，一般等於原始數據的標準差S。
高考標準分
我國普通高校全國招生統一考試所使用的標準分，就是用剛才介紹的方法進行轉換的。
即：
T=500+100Z
公式中取500為平均分，100為標準差
制度內容
建立標準分制度一般應由以下環節構成：①各省仍按以往的方法組織評分，然後合成每個考 生的各科原始分，並且統計各科的每個分數上的考生人數。②國家教委考試中心在部分省級 考試機構的配合下進行當年與往年的分數等值。
國家教委考試中心確定原始分數與標準分數的轉換關係， 各省考試機構根據轉換關係，得出省級常模量表分數。(各省在轉換時，可以根據分數分布 具體情況有些微調)③各省考試機構公布省級常模量表分數。(原始分不公布)
高考標準分數制度由常模量表分數(包括全國常模和省常模)、等值量表分數組成。具體講： 常模量表分數反映一次考試考生成績在考生總體中的位置，分數值與這一位置有關。由於高 考是全國統一考試，分省進行錄取，所以標準分數轉換有兩種情況：一種是把全國考生做為 一個總體進行分數轉換，另一種是把每個省的考生做為一個總體進行分數轉換，這樣建立的 常模量表分數能夠準確地刻劃考生成績在總體中的位置，使不同學科的成績能夠進行比較， 但還不能以此進行逐年的比較。為了彌補這種不足，就需要等值量表分數來完善。
理解使用
目的
常模轉換分數是根據高考的目的，按照常態分配的原理，把原始分數轉換成標準分數。這種 標準分數的平均分為500，標準差為100，每一常模轉換分數都與該分數以下的考生數與考生 總數的比例有確定的對應關係。
如某考生物理高考成績為690分，我們就可以查高考標準分與百分等級對照表，得出該考生 以下的考生占考生總數的比例。查表690分對應的比例為0.97127998(即97.127998%)，若該生為某省理工類考生，理工類考生數為9724人，則他超過9445人，比他分數高的考生約有279人(算法：9724×(1-0.97127998))，這樣我們很容易看出考生在全體考生中的位置，較精確地刻劃了考生在團體中的水平。另外，再次強調考生的各科成績和綜合分都是用常模量表分數來表示的，各科成績相加不等於綜合分。綜合分是根據各科標準分進行合成，然後按常模量表分數轉換方法得到的。請大家不要與原始總分混淆，也不要誤認為綜合分是各科標準分的平均分。
使用
在使用原始分的省份，考生得知自己的各科分數和總分後，就要用各類學校錄取分數線來衡 量自己的成績是上何類分數線，進而估計自己大概能上哪一類學校。但是在估計中，由於不 能知道自己在全體考生中的位置，所以往往盲目性很大。
使用標準分數以後，考生很容易得知自己的總成績和各科成績所處的位置，然後根據各類學 校錄取分數線在常模分數量表的位置，進而可以比較準確地估計和預測自己能上哪一類學校 ，把握有多大。
標準分轉換以後，考試機構在高考後送到考生手上的和在檔案中存放的是這樣的成績單：
成績通知單的含義是：
張華的綜合分為636，百分等級為913，則可知張華在全省理工類考生中的位置，即有91. 3%的考生成績比張華成績低。學科成績的含義與之相同。因為各學科成績具有同樣的參照點 ，所以我們還可以對各學科之間進行比較。這樣我們不難看出，張華的理綜較好，物理較差 。又如，某理工類考生綜合分為695分，對應的百分等級為974，當年理工類考生總數為110285人，在該生以上大約有2822人，而當年理工類本科錄取分數線為633人，對應的百分等級為908，則上線人數約為10120人，重點大學錄取分數線為658分，除掉多投檔的人數實際能錄5240人(即6228÷12=5240)。從以上情況分析，該生估計可能被重點大學錄取。但是，我們也應知道錄取新生既要看綜合分的高低，還要考查相關學科的成績，另外重要的一點要看考生所報志願學校的生源情況，考生在所報學校考生中的位置以及思想表現、身體狀況、高中畢業會考成績等情況。
(6)原始分轉換成標準分後的分數順序知：各科原始分轉換為標準分，每科成績的排列順序 不發生變化，即原始分高的標準分也高，原始分低的標準分也低，原始分相同的轉換後標準 分也相同。但綜合分的前後順序與原始總分的前後順序相比有一些變化。從總體上說原始總 分與綜合分一致性程度很高，雖然變動的範圍不大，但由於高校是“按總分劃線錄取的”， 人們自然會問：哪些考生不影響錄取，哪些考生影響錄取?綜合分這種前後次序的變動是否合理?
①高分段和低分段的考生。由於次序變化幅度很小，所以不管按哪種辦法計算總分，不影響 其是否錄取。也就是這說，優秀考生不管按什麼辦法算總分都會錄取，差生不管按什麼辦法 算總分，都不會被錄取。
②對總分處於最低錄取線邊緣的考生，由於原始分數算總分與標準分數算總分的方法不同， 兩種總分排序前後不同的幅度雖然不大，也會有少數考生出現錄取受到影響的情況，有的考 生原始分總分未上線，但轉換為標準分後上線了；有的考生原始分總分上線了，但轉換為標 準分後卻沒有上線。但總的來說，這種錄取受影響的情況所占考生的比例很小。
在原始分總分合成中，各科在總分中的權重是一種自然形成的結果。各科在總分中的權重取 決於各科分數分布的標準差的大小，標準差大(即考生分數分布比較分散，分數距離拉得比較大)，在總分中的權重就大，反之標準差小，在總分中的權重就小。也就是說在原始分中標準差大的，在總分累計中作用大，而標準差小的在總分中起作用小，這就使各科在錄取中應有的權重就不能體現出來。顯然，這種原始分累加計算總分是不合理的。使用標準分後，各科原始分轉換為平均分為500分，標準差為100分的標準分，各科分數就有共同的參照點，也有相同的單位，統一到同一“量尺”上的分數。這樣的各科標準分合成轉換為綜合分，保證了各科在總分中的權重，因此是合理的，上述少數學生錄取與否因轉化為標準綜合分後受到影響是正常的、合理的、科學的，這正是標準化制度克服原始分制度的缺點而顯示其優越性的結果。
相關說明
廣東省普通高考從上個世紀90年代初開始實行標準分。2007年因高中實行新課程改革，考生高考時可以選擇不同科目，選考X科的考生人數也不一樣，就改為使用原始分。而我市中考，每個考生的科目是相同的，實行標準分更為合理、科學，同時也有利於高中階段學校的招生選拔。
一、什麼是“原始分”？什麼是“標準分”？ 原始分是考試後直接從卷面上得到的分數。 標準分是指通過原始分轉化而得到的一種地位量數，它反映考生成績在全體考生成績中的位置。因此，無論試題難或易，無論整體原始分偏高或偏低，整體標準分都沒有什麼變化。
二、標準分是怎樣計算出來的？ 根據教育統計學的原理，標準分Z是原始分與平均分的離差以標準差為單位的分數，用公式表示為(右上角)
為該次考試中全體考生的平均分；X為該次考試中考生個人所得的原始分；S為該次考試分數的標準差。
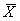
標準分有如下性質： ⑴平均值為0，標準差為1；
⑵分數之間等距，可以作加減運算；
⑶原始分轉換為標準分是線性轉換，不會改變原始分的分布形狀，也不改變原來分數的位置次序。 通過轉換後得到的標準分Z在一般情況下都帶小數，而且會出現負值，實際使用時不太方便，所以還要對Z分數進行線性變換（T變換）：
這就是我們通常所說的標準分。這種標準分的平均值為500，也就是說，如果某考生的標準分為500，則該生的成績處於此次考試的中間位置。 當然，這是在假定原始分呈常態分配的前提下進行的。如果原始分的分布不符合常態分配的要求，則要先進行正態化處理，再轉換為標準分，轉換後的分數稱為正態化標準分，這就是我們所稱的標準分數。
三、使用標準分比使用原始分有什麼好處？
根據教育統計學的原理，原始分轉換成標準分的意義可以從下面的比較中反映出來：
⑴單個標準分能夠反映考生成績在全體考生成績中的位置，而單個原始分則不能。 例如，某考生某科的原始成績為85分，無法說明其這科成績究竟如何，因為這與試題的難度有關，與總體考生的分數有關。如果某考生某科的標準分為650，即Z分數為1.5，則通過查常態分配表，查得對應的百分比為0.93319，於是我們知道，該考生的成績超過了93.319%的考生的成績，這就是分數解釋的標準化。
⑵不同學科的原始分不可比，而不同學科的標準分是可比的。 不同的學科，由於試題的難易程度不同，各學科的分數價值也就不同。例如某考生的語文原始成績為80分，數學原始成績為70分，從原始分看，其語文成績優於數學成績。但如果這次考試全體考生的語文原始分平均為86分，而數學原始分平均為60分，則該考生的語文成績處於全體考生的平均水平之下，而數學成績處於全體考生的平均水平之上，即該生的數學成績實質上優於語文成績。從標準分的角度來衡量，其語文標準分小於500分，而數學標準分大於500分。由於標準分代表了原始分在整體原始分中的位置，因此是可比的。
⑶不同學科的原始分不可加，而不同學科的標準分之間具有可加性。 既然不同學科的原始分不可比，那么也就不可加。多學科成績，只有在各科成績的平均值相同、標準差也相同的條件下，才能相加，否則是不科學的。各學科原始分的平均值以及標準差一般都不相同，而各學科的標準分的平均值以及標準差都基本相同，因此，各科的標準分是可加的。
四、標準總分是各科標準分的加權平均值嗎？
標準總分不是各科標準分的加權平均值。是將各科標準分進行加權相加，得到一個加權總和值（簡稱加權值），然後再將這個加權值轉換為標準分，所得值即為標準總分。
五、深圳市2008年中考成績以單科等級和標準總分同時呈現
我市中考也從上個世紀90年代開始實行標準分。十多年來，取得了較好的效果。2007年因受高考的影響，試用原始分，結果證明效果不甚理想。同一分數的考生上百人（如2007年中考總分為435分的考生，達300人之多），區分度較差，也不利於高中學校的錄取。我市決定今年中考仍使用標準分，學科統考成績以單科等級和標準總分同時呈現。單科等級成績根據單科標準分劃定，等級設定及各等級劃定比例為：
A+（5%）、A（20%）、B+（25%）、B（25%）、C+（20%）、C（5%）
標準總分由語文、數學、英語、科學、歷史與社會、體育六科標準分合成，其中語文、數學、英語、科學的權重均為1(從2013年以後科學權重1.5)，歷史與社會權重為0.6。體育成績以8%的權重計入中考標準總分（2008年體育成績權重5%）。10年體育以30%的權重計入中考標準總分
